A cutting plane algorithm for globally solving low dimensional k-means clustering problems

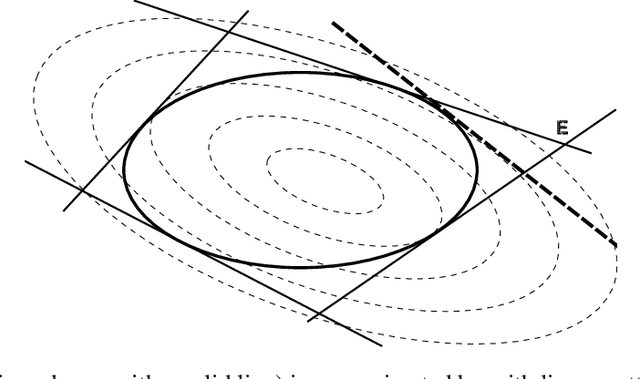
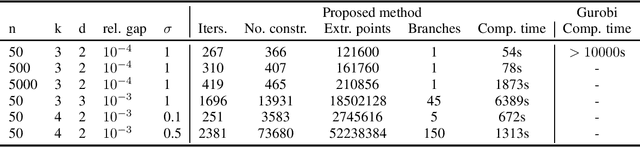
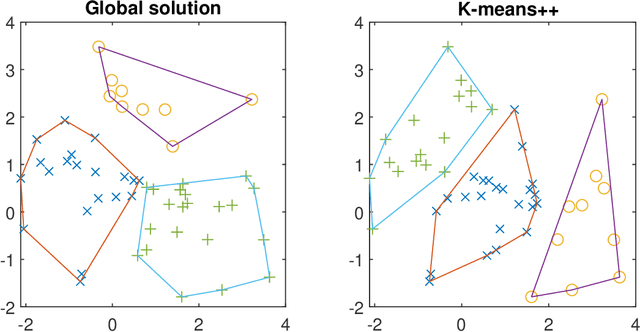
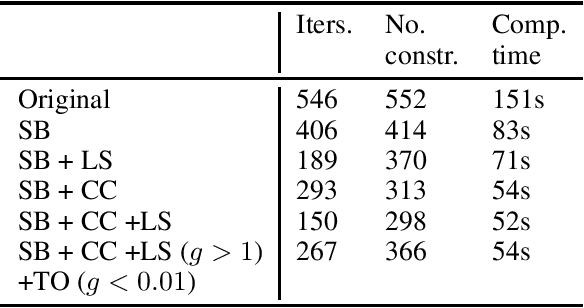
Clustering is one of the most fundamental tools in data science and machine learning, and k-means clustering is one of the most common such methods. There is a variety of approximate algorithms for the k-means problem, but computing the globally optimal solution is in general NP-hard. In this paper we consider the k-means problem for instances with low dimensional data and formulate it as a structured concave assignment problem. This allows us to exploit the low dimensional structure and solve the problem to global optimality within reasonable time for large data sets with several clusters. The method builds on iteratively solving a small concave problem and a large linear programming problem. This gives a sequence of feasible solutions along with bounds which we show converges to zero optimality gap. The paper combines methods from global optimization theory to accelerate the procedure, and we provide numerical results on their performance.

Globally solving the Gromov-Wasserstein problem for point clouds in low dimensional Euclidean spaces

This paper presents a framework for computing the Gromov-Wasserstein problem between two sets of points in low dimensional spaces, where the discrepancy is the squared Euclidean norm. The Gromov-Wasserstein problem is a generalization of the optimal transport problem that finds the assignment between two sets preserving pairwise distances as much as possible. This can be used to quantify the similarity between two formations or shapes, a common problem in AI and machine learning. The problem can be formulated as a Quadratic Assignment Problem (QAP), which is in general computationally intractable even for small problems. Our framework addresses this challenge by reformulating the QAP as an optimization problem with a low-dimensional domain, leveraging the fact that the problem can be expressed as a concave quadratic optimization problem with low rank. The method scales well with the number of points, and it can be used to find the global solution for large-scale problems with thousands of points. We compare the computational complexity of our approach with state-of-the-art methods on synthetic problems and apply it to a near-symmetrical problem which is of particular interest in computational biology.

Orthogonalization of data via Gromov-Wasserstein type feedback for clustering and visualization

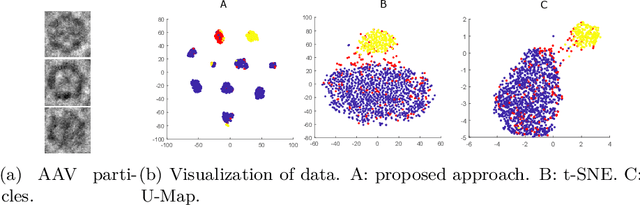
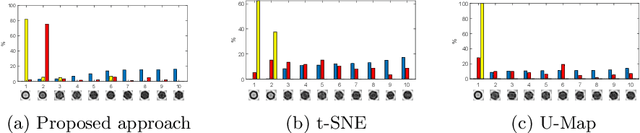
In this paper we propose an adaptive approach for clustering and visualization of data by an orthogonalization process. Starting with the data points being represented by a Markov process using the diffusion map framework, the method adaptively increase the orthogonality of the clusters by applying a feedback mechanism inspired by the Gromov-Wasserstein distance. This mechanism iteratively increases the spectral gap and refines the orthogonality of the data to achieve a clustering with high specificity. By using the diffusion map framework and representing the relation between data points using transition probabilities, the method is robust with respect to both the underlying distance, noise in the data and random initialization. We prove that the method converges globally to a unique fixpoint for certain parameter values. We also propose a related approach where the transition probabilities in the Markov process are required to be doubly stochastic, in which case the method generates a minimizer to a nonconvex optimization problem. We apply the method on cryo-electron microscopy image data from biopharmaceutical manufacturing where we can confirm biologically relevant insights related to therapeutic efficacy. We consider an example with morphological variations of gene packaging and confirm that the method produces biologically meaningful clustering results consistent with human expert classification.