Quantifying and Computing Covariance Uncertainty
Paper and Code
Oct 06, 2021
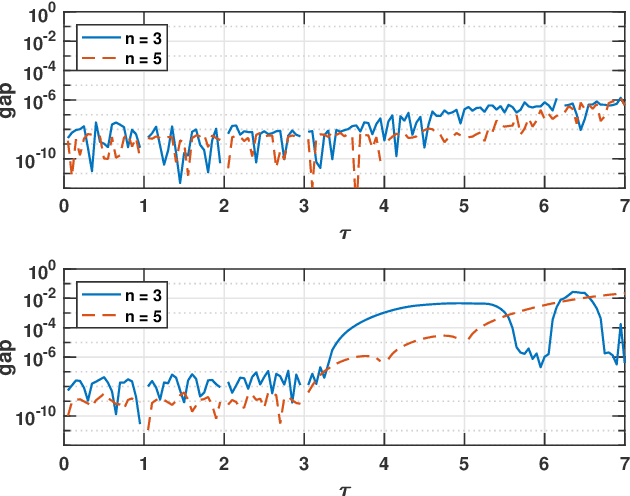
In this work, we consider the problem of bounding the values of a covariance function corresponding to a continuous-time stationary stochastic process or signal. Specifically, for two signals whose covariance functions agree on a finite discrete set of time-lags, we consider the maximal possible discrepancy of the covariance functions for real-valued time-lags outside this discrete grid. Computing this uncertainty corresponds to solving an infinite dimensional non-convex problem. However, we herein prove that the maximal objective value may be bounded from above by a finite dimensional convex optimization problem, allowing for efficient computation by standard methods. Furthermore, we empirically observe that for the case of signals whose spectra are supported on an interval, this upper bound is sharp, i.e., provides an exact quantification of the covariance uncertainty.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge