Manifold learning from a teacher's demonstrations

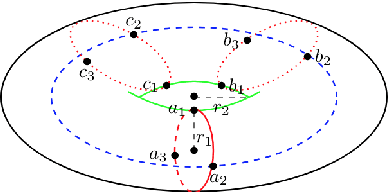
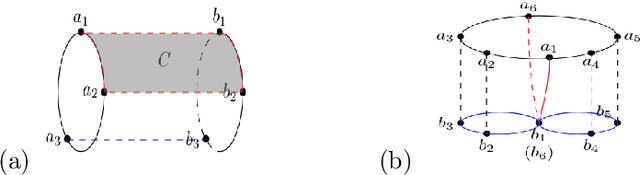
We consider the problem of manifold learning. Extending existing approaches of learning from randomly sampled data points, we consider contexts where data may be chosen by a teacher. We analyze learning from teachers who can provide structured data such as points, comparisons (pairs of points), demonstrations (sequences). We prove results showing that the former two do not yield notable decreases in the amount of data required to infer a manifold. Teaching by demonstration can yield remarkable decreases in the amount of data required, if we allow the goal to be teaching up to topology. We further analyze teaching learners in the context of persistence homology. Teaching topology can greatly reduce the number of datapoints required to infer correct geometry, and allows learning from teachers who themselves do not have full knowledge of the true manifold. We conclude with implications for learning in humans and machines.