Efficient Discretizations of Optimal Transport
Paper and Code
Feb 16, 2021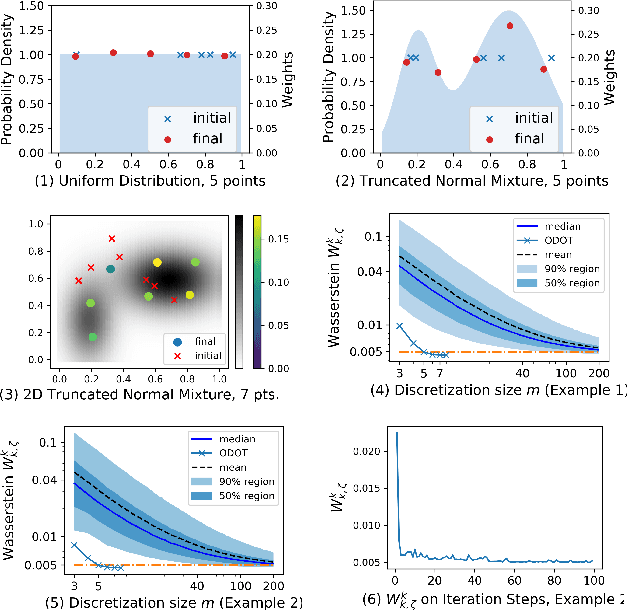

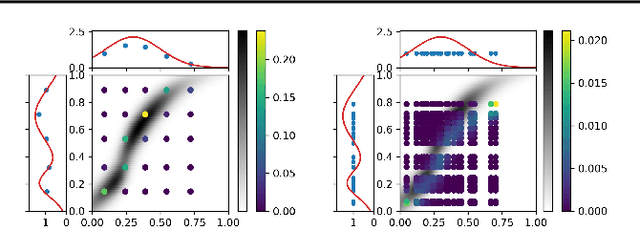
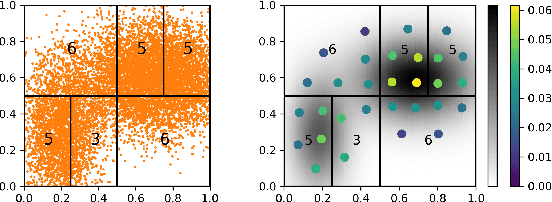
Obtaining solutions to Optimal Transportation (OT) problems is typically intractable when the marginal spaces are continuous. Recent research has focused on approximating continuous solutions with discretization methods based on i.i.d. sampling, and has proven convergence as the sample size increases. However, obtaining OT solutions with large sample sizes requires intensive computation effort, that can be prohibitive in practice. In this paper, we propose an algorithm for calculating discretizations with a given number of points for marginal distributions, by minimizing the (entropy-regularized) Wasserstein distance, and result in plans that are comparable to those obtained with much larger numbers of i.i.d. samples. Moreover, a local version of such discretizations which is parallelizable for large scale applications is proposed. We prove bounds for our approximation and demonstrate performance on a wide range of problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge