Small Models, Strong Priors: Architectural Inductive Bias for Parameter-Efficient Neural PDE Solvers

Neural PDE solvers have followed the scaling trajectory of vision and language, with recent foundation models reaching billions of parameters. We argue that scale is a poor substitute for architectural inductive bias in this domain: structured priors deliver outsized parameter efficiency, and the pattern of where they succeed and fail is itself informative about what they capture. We instantiate this argument in WaveLiT, an architecture combining a discrete wavelet transform for lossless multi-resolution tokenization, an augmented linear attention block, a shared-weight multiscale feature pyramid, and a wavelet-domain auxiliary loss. Bespoke 1-10M-parameter WaveLiT models compete with foundation models of 100-1000$\times$ their size across eight TheWell benchmarks, with the largest gains on wave and acoustic-dominated benchmarks where the wavelet-multiscale prior fits the dominant dynamical structure and small per-step errors do not compound geometrically under rollout. Trained jointly across all eight benchmarks, a 10M-parameter foundation variant exhibits a structured, physically interpretable transfer pattern -- strongest where the wavelet-multiscale prior matches the dynamics, weakest on chaotic advection-dominated flows. The entire pipeline trains on a single GPU. The results suggest that small-model PDE performance is shaped by architectural inductive bias rather than scale, and that the structure of a prior's failures is a useful empirical signal about its content.

Bridging Operator Learning and Conditioned Neural Fields: A Unifying Perspective

Operator learning is an emerging area of machine learning which aims to learn mappings between infinite dimensional function spaces. Here we uncover a connection between operator learning architectures and conditioned neural fields from computer vision, providing a unified perspective for examining differences between popular operator learning models. We find that many commonly used operator learning models can be viewed as neural fields with conditioning mechanisms restricted to point-wise and/or global information. Motivated by this, we propose the Continuous Vision Transformer (CViT), a novel neural operator architecture that employs a vision transformer encoder and uses cross-attention to modulate a base field constructed with a trainable grid-based positional encoding of query coordinates. Despite its simplicity, CViT achieves state-of-the-art results across challenging benchmarks in climate modeling and fluid dynamics. Our contributions can be viewed as a first step towards adapting advanced computer vision architectures for building more flexible and accurate machine learning models in physical sciences.

An Expert's Guide to Training Physics-informed Neural Networks

Physics-informed neural networks (PINNs) have been popularized as a deep learning framework that can seamlessly synthesize observational data and partial differential equation (PDE) constraints. Their practical effectiveness however can be hampered by training pathologies, but also oftentimes by poor choices made by users who lack deep learning expertise. In this paper we present a series of best practices that can significantly improve the training efficiency and overall accuracy of PINNs. We also put forth a series of challenging benchmark problems that highlight some of the most prominent difficulties in training PINNs, and present comprehensive and fully reproducible ablation studies that demonstrate how different architecture choices and training strategies affect the test accuracy of the resulting models. We show that the methods and guiding principles put forth in this study lead to state-of-the-art results and provide strong baselines that future studies should use for comparison purposes. To this end, we also release a highly optimized library in JAX that can be used to reproduce all results reported in this paper, enable future research studies, as well as facilitate easy adaptation to new use-case scenarios.

Respecting causality is all you need for training physics-informed neural networks

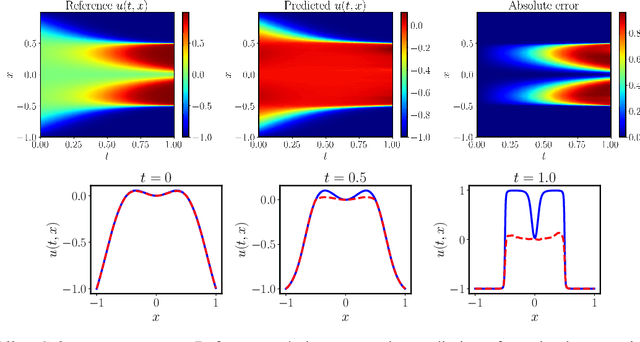
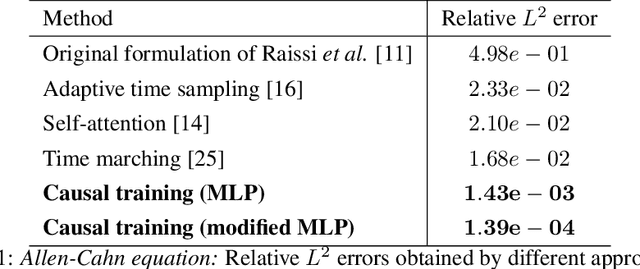
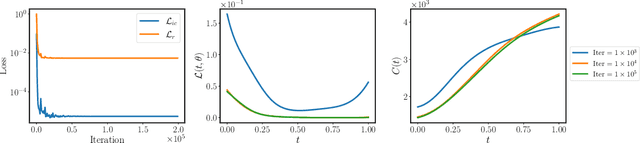
While the popularity of physics-informed neural networks (PINNs) is steadily rising, to this date PINNs have not been successful in simulating dynamical systems whose solution exhibits multi-scale, chaotic or turbulent behavior. In this work we attribute this shortcoming to the inability of existing PINNs formulations to respect the spatio-temporal causal structure that is inherent to the evolution of physical systems. We argue that this is a fundamental limitation and a key source of error that can ultimately steer PINN models to converge towards erroneous solutions. We address this pathology by proposing a simple re-formulation of PINNs loss functions that can explicitly account for physical causality during model training. We demonstrate that this simple modification alone is enough to introduce significant accuracy improvements, as well as a practical quantitative mechanism for assessing the convergence of a PINNs model. We provide state-of-the-art numerical results across a series of benchmarks for which existing PINNs formulations fail, including the chaotic Lorenz system, the Kuramoto-Sivashinsky equation in the chaotic regime, and the Navier-Stokes equations in the turbulent regime. To the best of our knowledge, this is the first time that PINNs have been successful in simulating such systems, introducing new opportunities for their applicability to problems of industrial complexity.