6-DoF Grasp Detection in Clutter with Enhanced Receptive Field and Graspable Balance Sampling

6-DoF grasp detection of small-scale grasps is crucial for robots to perform specific tasks. This paper focuses on enhancing the recognition capability of small-scale grasping, aiming to improve the overall accuracy of grasping prediction results and the generalization ability of the network. We propose an enhanced receptive field method that includes a multi-radii cylinder grouping module and a passive attention module. This method enhances the receptive field area within the graspable space and strengthens the learning of graspable features. Additionally, we design a graspable balance sampling module based on a segmentation network, which enables the network to focus on features of small objects, thereby improving the recognition capability of small-scale grasping. Our network achieves state-of-the-art performance on the GraspNet-1Billion dataset, with an overall improvement of approximately 10% in average precision@k (AP). Furthermore, we deployed our grasp detection model in pybullet grasping platform, which validates the effectiveness of our method.

Bridging Operator Learning and Conditioned Neural Fields: A Unifying Perspective

Operator learning is an emerging area of machine learning which aims to learn mappings between infinite dimensional function spaces. Here we uncover a connection between operator learning architectures and conditioned neural fields from computer vision, providing a unified perspective for examining differences between popular operator learning models. We find that many commonly used operator learning models can be viewed as neural fields with conditioning mechanisms restricted to point-wise and/or global information. Motivated by this, we propose the Continuous Vision Transformer (CViT), a novel neural operator architecture that employs a vision transformer encoder and uses cross-attention to modulate a base field constructed with a trainable grid-based positional encoding of query coordinates. Despite its simplicity, CViT achieves state-of-the-art results across challenging benchmarks in climate modeling and fluid dynamics. Our contributions can be viewed as a first step towards adapting advanced computer vision architectures for building more flexible and accurate machine learning models in physical sciences.

A Human-Machine Joint Learning Framework to Boost Endogenous BCI Training

Brain-computer interfaces (BCIs) provide a direct pathway from the brain to external devices and have demonstrated great potential for assistive and rehabilitation technologies. Endogenous BCIs based on electroencephalogram (EEG) signals, such as motor imagery (MI) BCIs, can provide some level of control. However, mastering spontaneous BCI control requires the users to generate discriminative and stable brain signal patterns by imagery, which is challenging and is usually achieved over a very long training time (weeks/months). Here, we propose a human-machine joint learning framework to boost the learning process in endogenous BCIs, by guiding the user to generate brain signals towards an optimal distribution estimated by the decoder, given the historical brain signals of the user. To this end, we firstly model the human-machine joint learning process in a uniform formulation. Then a human-machine joint learning framework is proposed: 1) for the human side, we model the learning process in a sequential trial-and-error scenario and propose a novel ``copy/new'' feedback paradigm to help shape the signal generation of the subject toward the optimal distribution; 2) for the machine side, we propose a novel adaptive learning algorithm to learn an optimal signal distribution along with the subject's learning process. Specifically, the decoder reweighs the brain signals generated by the subject to focus more on ``good'' samples to cope with the learning process of the subject. Online and psuedo-online BCI experiments with 18 healthy subjects demonstrated the advantages of the proposed joint learning process over co-adaptive approaches in both learning efficiency and effectiveness.

An Expert's Guide to Training Physics-informed Neural Networks

Physics-informed neural networks (PINNs) have been popularized as a deep learning framework that can seamlessly synthesize observational data and partial differential equation (PDE) constraints. Their practical effectiveness however can be hampered by training pathologies, but also oftentimes by poor choices made by users who lack deep learning expertise. In this paper we present a series of best practices that can significantly improve the training efficiency and overall accuracy of PINNs. We also put forth a series of challenging benchmark problems that highlight some of the most prominent difficulties in training PINNs, and present comprehensive and fully reproducible ablation studies that demonstrate how different architecture choices and training strategies affect the test accuracy of the resulting models. We show that the methods and guiding principles put forth in this study lead to state-of-the-art results and provide strong baselines that future studies should use for comparison purposes. To this end, we also release a highly optimized library in JAX that can be used to reproduce all results reported in this paper, enable future research studies, as well as facilitate easy adaptation to new use-case scenarios.

Random Weight Factorization Improves the Training of Continuous Neural Representations

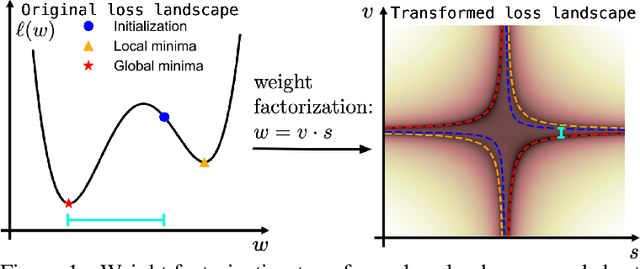
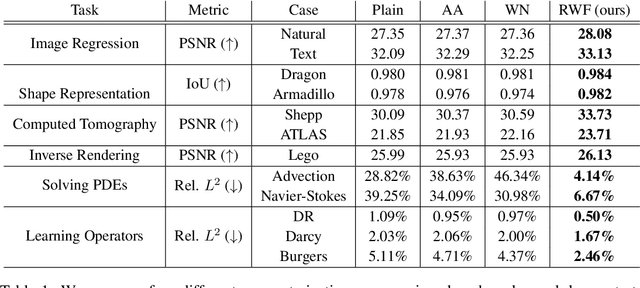
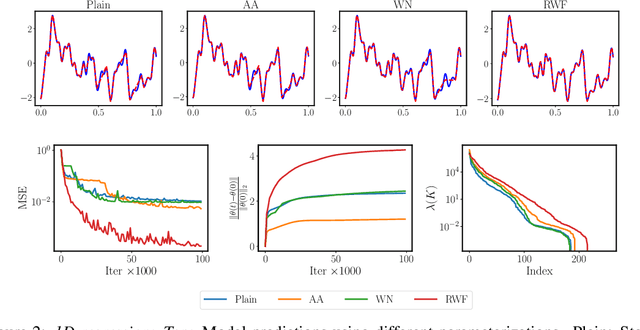
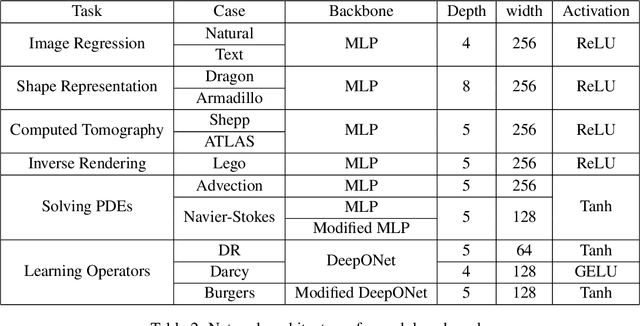
Continuous neural representations have recently emerged as a powerful and flexible alternative to classical discretized representations of signals. However, training them to capture fine details in multi-scale signals is difficult and computationally expensive. Here we propose random weight factorization as a simple drop-in replacement for parameterizing and initializing conventional linear layers in coordinate-based multi-layer perceptrons (MLPs) that significantly accelerates and improves their training. We show how this factorization alters the underlying loss landscape and effectively enables each neuron in the network to learn using its own self-adaptive learning rate. This not only helps with mitigating spectral bias, but also allows networks to quickly recover from poor initializations and reach better local minima. We demonstrate how random weight factorization can be leveraged to improve the training of neural representations on a variety of tasks, including image regression, shape representation, computed tomography, inverse rendering, solving partial differential equations, and learning operators between function spaces.

Improved architectures and training algorithms for deep operator networks

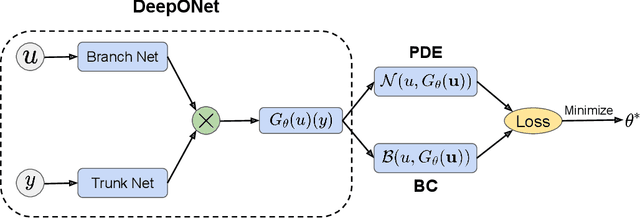
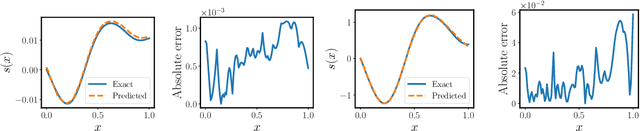
Operator learning techniques have recently emerged as a powerful tool for learning maps between infinite-dimensional Banach spaces. Trained under appropriate constraints, they can also be effective in learning the solution operator of partial differential equations (PDEs) in an entirely self-supervised manner. In this work we analyze the training dynamics of deep operator networks (DeepONets) through the lens of Neural Tangent Kernel (NTK) theory, and reveal a bias that favors the approximation of functions with larger magnitudes. To correct this bias we propose to adaptively re-weight the importance of each training example, and demonstrate how this procedure can effectively balance the magnitude of back-propagated gradients during training via gradient descent. We also propose a novel network architecture that is more resilient to vanishing gradient pathologies. Taken together, our developments provide new insights into the training of DeepONets and consistently improve their predictive accuracy by a factor of 10-50x, demonstrated in the challenging setting of learning PDE solution operators in the absence of paired input-output observations. All code and data accompanying this manuscript are publicly available at \url{https://github.com/PredictiveIntelligenceLab/ImprovedDeepONets.}

Learning the solution operator of parametric partial differential equations with physics-informed DeepOnets

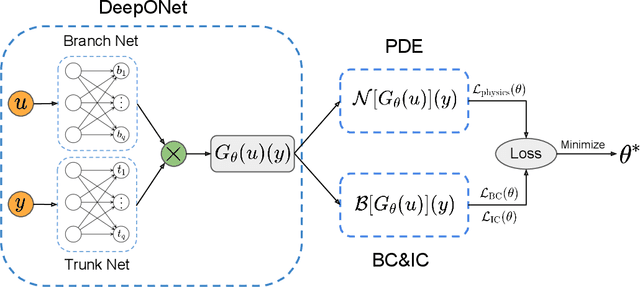
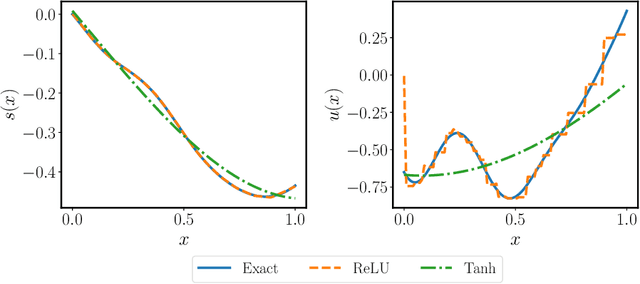
Deep operator networks (DeepONets) are receiving increased attention thanks to their demonstrated capability to approximate nonlinear operators between infinite-dimensional Banach spaces. However, despite their remarkable early promise, they typically require large training data-sets consisting of paired input-output observations which may be expensive to obtain, while their predictions may not be consistent with the underlying physical principles that generated the observed data. In this work, we propose a novel model class coined as physics-informed DeepONets, which introduces an effective regularization mechanism for biasing the outputs of DeepOnet models towards ensuring physical consistency. This is accomplished by leveraging automatic differentiation to impose the underlying physical laws via soft penalty constraints during model training. We demonstrate that this simple, yet remarkably effective extension can not only yield a significant improvement in the predictive accuracy of DeepOnets, but also greatly reduce the need for large training data-sets. To this end, a remarkable observation is that physics-informed DeepONets are capable of solving parametric partial differential equations (PDEs) without any paired input-output observations, except for a set of given initial or boundary conditions. We illustrate the effectiveness of the proposed framework through a series of comprehensive numerical studies across various types of PDEs. Strikingly, a trained physics informed DeepOnet model can predict the solution of $\mathcal{O}(10^3)$ time-dependent PDEs in a fraction of a second -- up to three orders of magnitude faster compared a conventional PDE solver. The data and code accompanying this manuscript are publicly available at \url{https://github.com/PredictiveIntelligenceLab/Physics-informed-DeepONets}.

On the eigenvector bias of Fourier feature networks: From regression to solving multi-scale PDEs with physics-informed neural networks

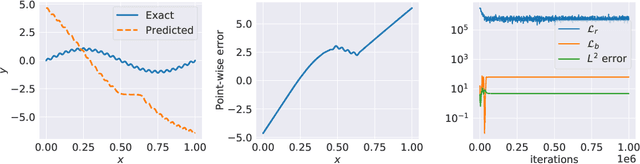
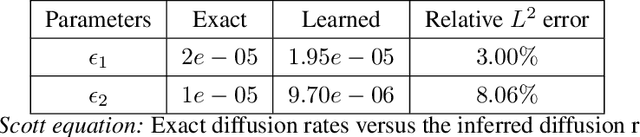
Physics-informed neural networks (PINNs) are demonstrating remarkable promise in integrating physical models with gappy and noisy observational data, but they still struggle in cases where the target functions to be approximated exhibit high-frequency or multi-scale features. In this work we investigate this limitation through the lens of Neural Tangent Kernel (NTK) theory and elucidate how PINNs are biased towards learning functions along the dominant eigen-directions of their limiting NTK. Using this observation, we construct novel architectures that employ spatio-temporal and multi-scale random Fourier features, and justify how such coordinate embedding layers can lead to robust and accurate PINN models. Numerical examples are presented for several challenging cases where conventional PINN models fail, including wave propagation and reaction-diffusion dynamics, illustrating how the proposed methods can be used to effectively tackle both forward and inverse problems involving partial differential equations with multi-scale behavior. All code an data accompanying this manuscript will be made publicly available at \url{https://github.com/PredictiveIntelligenceLab/MultiscalePINNs}.