Improved architectures and training algorithms for deep operator networks
Paper and Code
Oct 11, 2021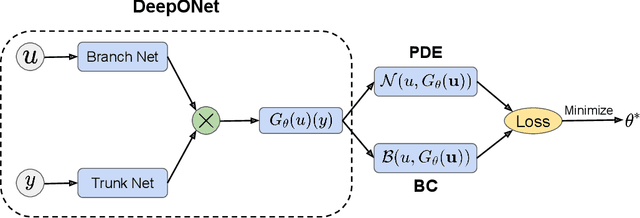

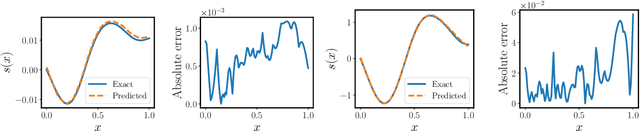

Operator learning techniques have recently emerged as a powerful tool for learning maps between infinite-dimensional Banach spaces. Trained under appropriate constraints, they can also be effective in learning the solution operator of partial differential equations (PDEs) in an entirely self-supervised manner. In this work we analyze the training dynamics of deep operator networks (DeepONets) through the lens of Neural Tangent Kernel (NTK) theory, and reveal a bias that favors the approximation of functions with larger magnitudes. To correct this bias we propose to adaptively re-weight the importance of each training example, and demonstrate how this procedure can effectively balance the magnitude of back-propagated gradients during training via gradient descent. We also propose a novel network architecture that is more resilient to vanishing gradient pathologies. Taken together, our developments provide new insights into the training of DeepONets and consistently improve their predictive accuracy by a factor of 10-50x, demonstrated in the challenging setting of learning PDE solution operators in the absence of paired input-output observations. All code and data accompanying this manuscript are publicly available at \url{https://github.com/PredictiveIntelligenceLab/ImprovedDeepONets.}
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge