Xiaotian Gao
NeuralStagger: accelerating physics-constrained neural PDE solver with spatial-temporal decomposition
Feb 20, 2023Abstract:Neural networks have shown great potential in accelerating the solution of partial differential equations (PDEs). Recently, there has been a growing interest in introducing physics constraints into training neural PDE solvers to reduce the use of costly data and improve the generalization ability. However, these physics constraints, based on certain finite dimensional approximations over the function space, must resolve the smallest scaled physics to ensure the accuracy and stability of the simulation, resulting in high computational costs from large input, output, and neural networks. This paper proposes a general acceleration methodology called NeuralStagger by spatially and temporally decomposing the original learning tasks into several coarser-resolution subtasks. We define a coarse-resolution neural solver for each subtask, which requires fewer computational resources, and jointly train them with the vanilla physics-constrained loss by simply arranging their outputs to reconstruct the original solution. Due to the perfect parallelism between them, the solution is achieved as fast as a coarse-resolution neural solver. In addition, the trained solvers bring the flexibility of simulating with multiple levels of resolution. We demonstrate the successful application of NeuralStagger on 2D and 3D fluid dynamics simulations, which leads to an additional $10\sim100\times$ speed-up. Moreover, the experiment also shows that the learned model could be well used for optimal control.
Efficient Activation Quantization via Adaptive Rounding Border for Post-Training Quantization
Aug 25, 2022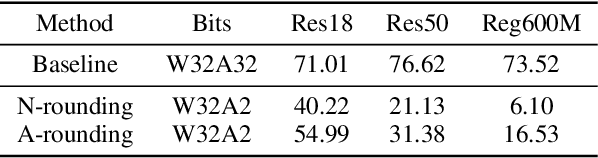
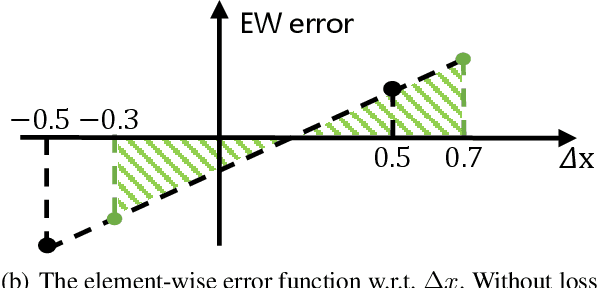
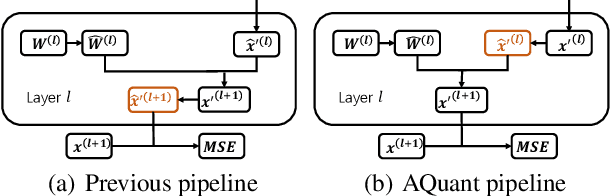
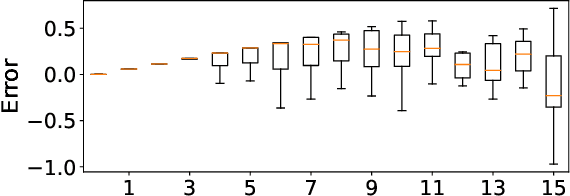
Abstract:Post-training quantization (PTQ) attracts increasing attention due to its convenience in deploying quantized neural networks. Rounding, the primary source of quantization error, is optimized only for model weights, while activations still use the rounding-to-nearest operation. In this work, for the first time, we demonstrate that well-chosen rounding schemes for activations can improve the final accuracy. To deal with the challenge of the dynamicity of the activation rounding scheme, we adaptively adjust the rounding border through a simple function to generate rounding schemes at the inference stage. The border function covers the impact of weight errors, activation errors, and propagated errors to eliminate the bias of the element-wise error, which further benefits model accuracy. We also make the border aware of global errors to better fit different arriving activations. Finally, we propose the AQuant framework to learn the border function. Extensive experiments show that AQuant achieves noticeable improvements with negligible overhead compared with state-of-the-art works and pushes the accuracy of ResNet-18 up to 60.3\% under the 2-bit weight and activation post-training quantization.
LordNet: Learning to Solve Parametric Partial Differential Equations without Simulated Data
Jun 19, 2022



Abstract:Neural operators, as a powerful approximation to the non-linear operators between infinite-dimensional function spaces, have proved to be promising in accelerating the solution of partial differential equations (PDE). However, it requires a large amount of simulated data which can be costly to collect, resulting in a chicken-egg dilemma and limiting its usage in solving PDEs. To jump out of the dilemma, we propose a general data-free paradigm where the neural network directly learns physics from the mean squared residual (MSR) loss constructed by the discretized PDE. We investigate the physical information in the MSR loss and identify the challenge that the neural network must have the capacity to model the long range entanglements in the spatial domain of the PDE, whose patterns vary in different PDEs. Therefore, we propose the low-rank decomposition network (LordNet) which is tunable and also efficient to model various entanglements. Specifically, LordNet learns a low-rank approximation to the global entanglements with simple fully connected layers, which extracts the dominant pattern with reduced computational cost. The experiments on solving Poisson's equation and Navier-Stokes equation demonstrate that the physical constraints by the MSR loss can lead to better accuracy and generalization ability of the neural network. In addition, LordNet outperforms other modern neural network architectures in both PDEs with the fewest parameters and the fastest inference speed. For Navier-Stokes equation, the learned operator is over 50 times faster than the finite difference solution with the same computational resources.
Learning Physics-Informed Neural Networks without Stacked Back-propagation
Feb 18, 2022



Abstract:Physics-Informed Neural Network (PINN) has become a commonly used machine learning approach to solve partial differential equations (PDE). But, facing high-dimensional second-order PDE problems, PINN will suffer from severe scalability issues since its loss includes second-order derivatives, the computational cost of which will grow along with the dimension during stacked back-propagation. In this paper, we develop a novel approach that can significantly accelerate the training of Physics-Informed Neural Networks. In particular, we parameterize the PDE solution by the Gaussian smoothed model and show that, derived from Stein's Identity, the second-order derivatives can be efficiently calculated without back-propagation. We further discuss the model capacity and provide variance reduction methods to address key limitations in the derivative estimation. Experimental results show that our proposed method can achieve competitive error compared to standard PINN training but is two orders of magnitude faster.
SQuant: On-the-Fly Data-Free Quantization via Diagonal Hessian Approximation
Feb 14, 2022



Abstract:Quantization of deep neural networks (DNN) has been proven effective for compressing and accelerating DNN models. Data-free quantization (DFQ) is a promising approach without the original datasets under privacy-sensitive and confidential scenarios. However, current DFQ solutions degrade accuracy, need synthetic data to calibrate networks, and are time-consuming and costly. This paper proposes an on-the-fly DFQ framework with sub-second quantization time, called SQuant, which can quantize networks on inference-only devices with low computation and memory requirements. With the theoretical analysis of the second-order information of DNN task loss, we decompose and approximate the Hessian-based optimization objective into three diagonal sub-items, which have different areas corresponding to three dimensions of weight tensor: element-wise, kernel-wise, and output channel-wise. Then, we progressively compose sub-items and propose a novel data-free optimization objective in the discrete domain, minimizing Constrained Absolute Sum of Error (or CASE in short), which surprisingly does not need any dataset and is even not aware of network architecture. We also design an efficient algorithm without back-propagation to further reduce the computation complexity of the objective solver. Finally, without fine-tuning and synthetic datasets, SQuant accelerates the data-free quantization process to a sub-second level with >30% accuracy improvement over the existing data-free post-training quantization works, with the evaluated models under 4-bit quantization. We have open-sourced the SQuant framework at https://github.com/clevercool/SQuant.
AceNAS: Learning to Rank Ace Neural Architectures with Weak Supervision of Weight Sharing
Aug 06, 2021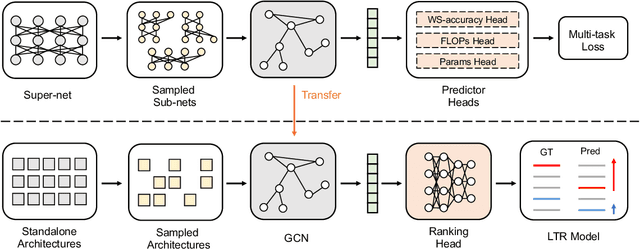
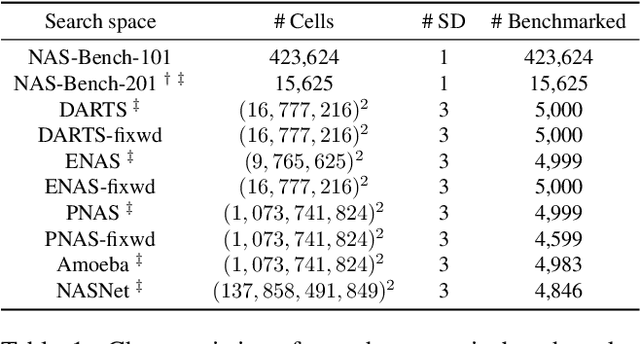
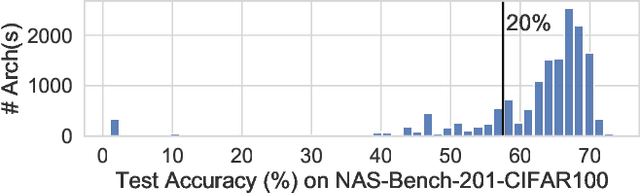
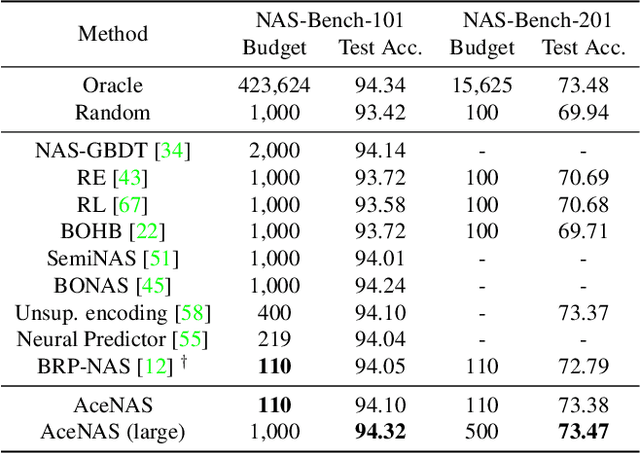
Abstract:Architecture performance predictors have been widely used in neural architecture search (NAS). Although they are shown to be simple and effective, the optimization objectives in previous arts (e.g., precise accuracy estimation or perfect ranking of all architectures in the space) did not capture the ranking nature of NAS. In addition, a large number of ground-truth architecture-accuracy pairs are usually required to build a reliable predictor, making the process too computationally expensive. To overcome these, in this paper, we look at NAS from a novel point of view and introduce Learning to Rank (LTR) methods to select the best (ace) architectures from a space. Specifically, we propose to use Normalized Discounted Cumulative Gain (NDCG) as the target metric and LambdaRank as the training algorithm. We also propose to leverage weak supervision from weight sharing by pretraining architecture representation on weak labels obtained from the super-net and then finetuning the ranking model using a small number of architectures trained from scratch. Extensive experiments on NAS benchmarks and large-scale search spaces demonstrate that our approach outperforms SOTA with a significantly reduced search cost.
OpEvo: An Evolutionary Method for Tensor Operator Optimization
Jun 10, 2020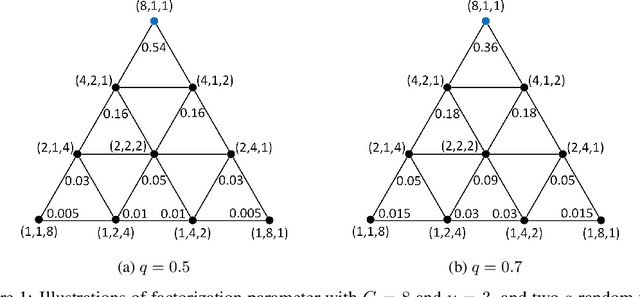
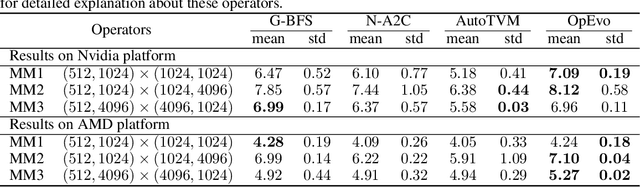
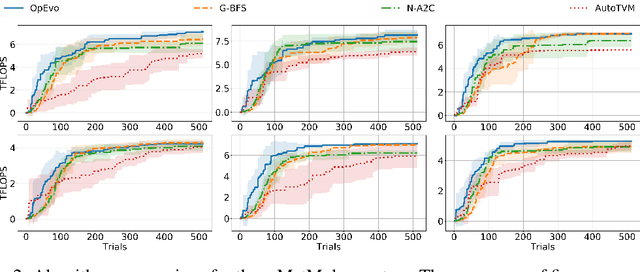
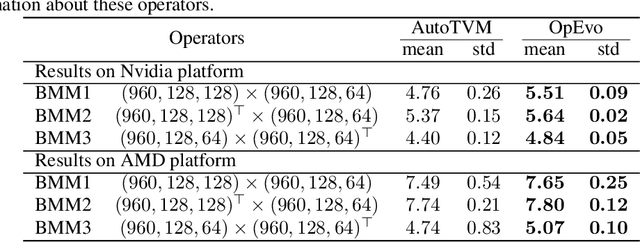
Abstract:Training and inference efficiency of deep neural networks highly rely on the performance of tensor operators on hardware platforms. Manually optimized tensor operators have limitations in terms of supporting new operators or supporting new hardware platforms. Therefore, automatically optimizing device code configurations of tensor operators is getting increasingly attractive. However, current methods for tensor operator optimization usually suffer from poor sample-efficiency due to the combinatorial search space. In this work, we propose a novel evolutionary method, OpEvo, which efficiently explores the search spaces of tensor operators by introducing a topology-aware mutation operation based on q-random walk distribution to leverage the topological structures over the search spaces. Our comprehensive experiment results show that OpEvo can find the best configuration with the least number of trials and the lowest variance compared with state-of-the-art methods. All code of this work is available online.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge