Enhancing the Scalability and Applicability of Kohn-Sham Hamiltonians for Molecular Systems

Density Functional Theory (DFT) is a pivotal method within quantum chemistry and materials science, with its core involving the construction and solution of the Kohn-Sham Hamiltonian. Despite its importance, the application of DFT is frequently limited by the substantial computational resources required to construct the Kohn-Sham Hamiltonian. In response to these limitations, current research has employed deep-learning models to efficiently predict molecular and solid Hamiltonians, with roto-translational symmetries encoded in their neural networks. However, the scalability of prior models may be problematic when applied to large molecules, resulting in non-physical predictions of ground-state properties. In this study, we generate a substantially larger training set (PubChemQH) than used previously and use it to create a scalable model for DFT calculations with physical accuracy. For our model, we introduce a loss function derived from physical principles, which we call Wavefunction Alignment Loss (WALoss). WALoss involves performing a basis change on the predicted Hamiltonian to align it with the observed one; thus, the resulting differences can serve as a surrogate for orbital energy differences, allowing models to make better predictions for molecular orbitals and total energies than previously possible. WALoss also substantially accelerates self-consistent-field (SCF) DFT calculations. Here, we show it achieves a reduction in total energy prediction error by a factor of 1347 and an SCF calculation speed-up by a factor of 18%. These substantial improvements set new benchmarks for achieving accurate and applicable predictions in larger molecular systems.

Efficient and Scalable Density Functional Theory Hamiltonian Prediction through Adaptive Sparsity

Hamiltonian matrix prediction is pivotal in computational chemistry, serving as the foundation for determining a wide range of molecular properties. While SE(3) equivariant graph neural networks have achieved remarkable success in this domain, their substantial computational cost-driven by high-order tensor product (TP) operations-restricts their scalability to large molecular systems with extensive basis sets. To address this challenge, we introduce SPHNet, an efficient and scalable equivariant network that incorporates adaptive sparsity into Hamiltonian prediction. SPHNet employs two innovative sparse gates to selectively constrain non-critical interaction combinations, significantly reducing tensor product computations while maintaining accuracy. To optimize the sparse representation, we develop a Three-phase Sparsity Scheduler, ensuring stable convergence and achieving high performance at sparsity rates of up to 70 percent. Extensive evaluations on QH9 and PubchemQH datasets demonstrate that SPHNet achieves state-of-the-art accuracy while providing up to a 7x speedup over existing models. Beyond Hamiltonian prediction, the proposed sparsification techniques also hold significant potential for improving the efficiency and scalability of other SE(3) equivariant networks, further broadening their applicability and impact.

\underline{E2}Former: A Linear-time \underline{E}fficient and \underline{E}quivariant Trans\underline{former} for Scalable Molecular Modeling

Equivariant Graph Neural Networks (EGNNs) have demonstrated significant success in modeling microscale systems, including those in chemistry, biology and materials science. However, EGNNs face substantial computational challenges due to the high cost of constructing edge features via spherical tensor products, making them impractical for large-scale systems. To address this limitation, we introduce E2Former, an equivariant and efficient transformer architecture that incorporates the Wigner $6j$ convolution (Wigner $6j$ Conv). By shifting the computational burden from edges to nodes, the Wigner $6j$ Conv reduces the complexity from $O(|\mathcal{E}|)$ to $ O(| \mathcal{V}|)$ while preserving both the model's expressive power and rotational equivariance. We show that this approach achieves a 7x-30x speedup compared to conventional $\mathrm{SO}(3)$ convolutions. Furthermore, our empirical results demonstrate that the derived E2Former mitigates the computational challenges of existing approaches without compromising the ability to capture detailed geometric information. This development could suggest a promising direction for scalable and efficient molecular modeling.

Infusing Self-Consistency into Density Functional Theory Hamiltonian Prediction via Deep Equilibrium Models

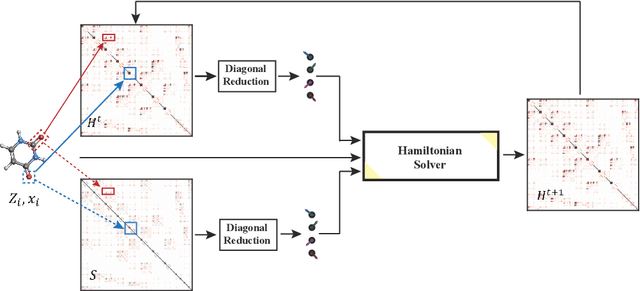
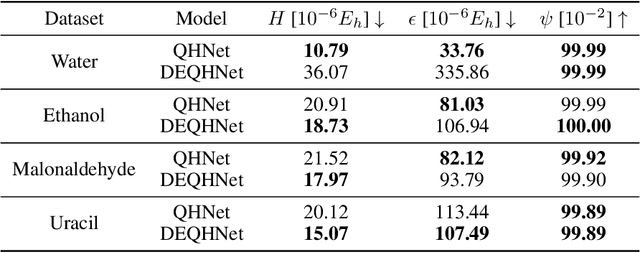
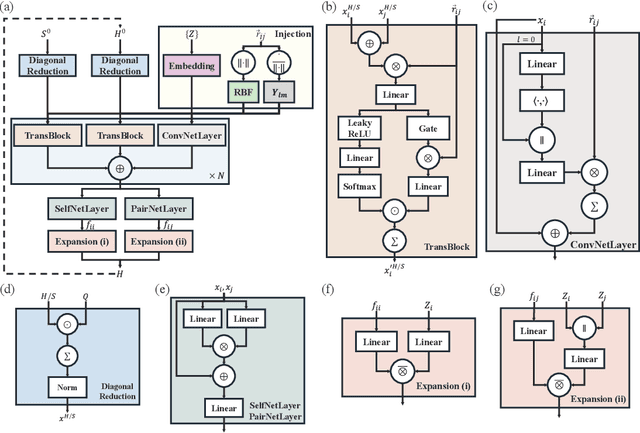
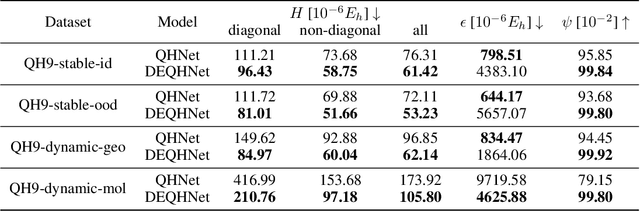
In this study, we introduce a unified neural network architecture, the Deep Equilibrium Density Functional Theory Hamiltonian (DEQH) model, which incorporates Deep Equilibrium Models (DEQs) for predicting Density Functional Theory (DFT) Hamiltonians. The DEQH model inherently captures the self-consistency nature of Hamiltonian, a critical aspect often overlooked by traditional machine learning approaches for Hamiltonian prediction. By employing DEQ within our model architecture, we circumvent the need for DFT calculations during the training phase to introduce the Hamiltonian's self-consistency, thus addressing computational bottlenecks associated with large or complex systems. We propose a versatile framework that combines DEQ with off-the-shelf machine learning models for predicting Hamiltonians. When benchmarked on the MD17 and QH9 datasets, DEQHNet, an instantiation of the DEQH framework, has demonstrated a significant improvement in prediction accuracy. Beyond a predictor, the DEQH model is a Hamiltonian solver, in the sense that it uses the fixed-point solving capability of the deep equilibrium model to iteratively solve for the Hamiltonian. Ablation studies of DEQHNet further elucidate the network's effectiveness, offering insights into the potential of DEQ-integrated networks for Hamiltonian learning.

Self-Consistency Training for Hamiltonian Prediction

Hamiltonian prediction is a versatile formulation to leverage machine learning for solving molecular science problems. Yet, its applicability is limited by insufficient labeled data for training. In this work, we highlight that Hamiltonian prediction possesses a self-consistency principle, based on which we propose an exact training method that does not require labeled data. This merit addresses the data scarcity difficulty, and distinguishes the task from other property prediction formulations with unique benefits: (1) self-consistency training enables the model to be trained on a large amount of unlabeled data, hence substantially enhances generalization; (2) self-consistency training is more efficient than labeling data with DFT for supervised training, since it is an amortization of DFT calculation over a set of molecular structures. We empirically demonstrate the better generalization in data-scarce and out-of-distribution scenarios, and the better efficiency from the amortization. These benefits push forward the applicability of Hamiltonian prediction to an ever larger scale.

AI Agent as Urban Planner: Steering Stakeholder Dynamics in Urban Planning via Consensus-based Multi-Agent Reinforcement Learning

In urban planning, land use readjustment plays a pivotal role in aligning land use configurations with the current demands for sustainable urban development. However, present-day urban planning practices face two main issues. Firstly, land use decisions are predominantly dependent on human experts. Besides, while resident engagement in urban planning can promote urban sustainability and livability, it is challenging to reconcile the diverse interests of stakeholders. To address these challenges, we introduce a Consensus-based Multi-Agent Reinforcement Learning framework for real-world land use readjustment. This framework serves participatory urban planning, allowing diverse intelligent agents as stakeholder representatives to vote for preferred land use types. Within this framework, we propose a novel consensus mechanism in reward design to optimize land utilization through collective decision making. To abstract the structure of the complex urban system, the geographic information of cities is transformed into a spatial graph structure and then processed by graph neural networks. Comprehensive experiments on both traditional top-down planning and participatory planning methods from real-world communities indicate that our computational framework enhances global benefits and accommodates diverse interests, leading to improved satisfaction across different demographic groups. By integrating Multi-Agent Reinforcement Learning, our framework ensures that participatory urban planning decisions are more dynamic and adaptive to evolving community needs and provides a robust platform for automating complex real-world urban planning processes.

LordNet: Learning to Solve Parametric Partial Differential Equations without Simulated Data

Neural operators, as a powerful approximation to the non-linear operators between infinite-dimensional function spaces, have proved to be promising in accelerating the solution of partial differential equations (PDE). However, it requires a large amount of simulated data which can be costly to collect, resulting in a chicken-egg dilemma and limiting its usage in solving PDEs. To jump out of the dilemma, we propose a general data-free paradigm where the neural network directly learns physics from the mean squared residual (MSR) loss constructed by the discretized PDE. We investigate the physical information in the MSR loss and identify the challenge that the neural network must have the capacity to model the long range entanglements in the spatial domain of the PDE, whose patterns vary in different PDEs. Therefore, we propose the low-rank decomposition network (LordNet) which is tunable and also efficient to model various entanglements. Specifically, LordNet learns a low-rank approximation to the global entanglements with simple fully connected layers, which extracts the dominant pattern with reduced computational cost. The experiments on solving Poisson's equation and Navier-Stokes equation demonstrate that the physical constraints by the MSR loss can lead to better accuracy and generalization ability of the neural network. In addition, LordNet outperforms other modern neural network architectures in both PDEs with the fewest parameters and the fastest inference speed. For Navier-Stokes equation, the learned operator is over 50 times faster than the finite difference solution with the same computational resources.

Cooperative Policy Learning with Pre-trained Heterogeneous Observation Representations

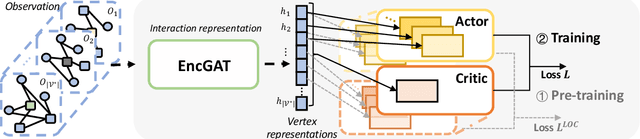
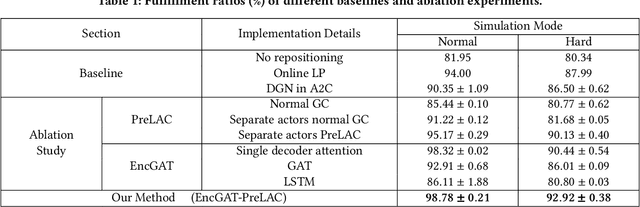
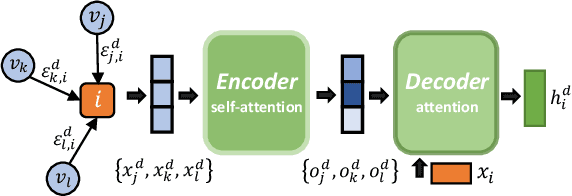
Multi-agent reinforcement learning (MARL) has been increasingly explored to learn the cooperative policy towards maximizing a certain global reward. Many existing studies take advantage of graph neural networks (GNN) in MARL to propagate critical collaborative information over the interaction graph, built upon inter-connected agents. Nevertheless, the vanilla GNN approach yields substantial defects in dealing with complex real-world scenarios since the generic message passing mechanism is ineffective between heterogeneous vertices and, moreover, simple message aggregation functions are incapable of accurately modeling the combinational interactions from multiple neighbors. While adopting complex GNN models with more informative message passing and aggregation mechanisms can obviously benefit heterogeneous vertex representations and cooperative policy learning, it could, on the other hand, increase the training difficulty of MARL and demand more intense and direct reward signals compared to the original global reward. To address these challenges, we propose a new cooperative learning framework with pre-trained heterogeneous observation representations. Particularly, we employ an encoder-decoder based graph attention to learn the intricate interactions and heterogeneous representations that can be more easily leveraged by MARL. Moreover, we design a pre-training with local actor-critic algorithm to ease the difficulty in cooperative policy learning. Extensive experiments over real-world scenarios demonstrate that our new approach can significantly outperform existing MARL baselines as well as operational research solutions that are widely-used in industry.