Reveal the Mystery of DPO: The Connection between DPO and RL Algorithms

With the rapid development of Large Language Models (LLMs), numerous Reinforcement Learning from Human Feedback (RLHF) algorithms have been introduced to improve model safety and alignment with human preferences. These algorithms can be divided into two main frameworks based on whether they require an explicit reward (or value) function for training: actor-critic-based Proximal Policy Optimization (PPO) and alignment-based Direct Preference Optimization (DPO). The mismatch between DPO and PPO, such as DPO's use of a classification loss driven by human-preferred data, has raised confusion about whether DPO should be classified as a Reinforcement Learning (RL) algorithm. To address these ambiguities, we focus on three key aspects related to DPO, RL, and other RLHF algorithms: (1) the construction of the loss function; (2) the target distribution at which the algorithm converges; (3) the impact of key components within the loss function. Specifically, we first establish a unified framework named UDRRA connecting these algorithms based on the construction of their loss functions. Next, we uncover their target policy distributions within this framework. Finally, we investigate the critical components of DPO to understand their impact on the convergence rate. Our work provides a deeper understanding of the relationship between DPO, RL, and other RLHF algorithms, offering new insights for improving existing algorithms.

Enhancing Text-to-Image Editing via Hybrid Mask-Informed Fusion

Recently, text-to-image (T2I) editing has been greatly pushed forward by applying diffusion models. Despite the visual promise of the generated images, inconsistencies with the expected textual prompt remain prevalent. This paper aims to systematically improve the text-guided image editing techniques based on diffusion models, by addressing their limitations. Notably, the common idea in diffusion-based editing firstly reconstructs the source image via inversion techniques e.g., DDIM Inversion. Then following a fusion process that carefully integrates the source intermediate (hidden) states (obtained by inversion) with the ones of the target image. Unfortunately, such a standard pipeline fails in many cases due to the interference of texture retention and the new characters creation in some regions. To mitigate this, we incorporate human annotation as an external knowledge to confine editing within a ``Mask-informed'' region. Then we carefully Fuse the edited image with the source image and a constructed intermediate image within the model's Self-Attention module. Extensive empirical results demonstrate the proposed ``MaSaFusion'' significantly improves the existing T2I editing techniques.

Towards Understanding the Working Mechanism of Text-to-Image Diffusion Model

Recently, the strong latent Diffusion Probabilistic Model (DPM) has been applied to high-quality Text-to-Image (T2I) generation (e.g., Stable Diffusion), by injecting the encoded target text prompt into the gradually denoised diffusion image generator. Despite the success of DPM in practice, the mechanism behind it remains to be explored. To fill this blank, we begin by examining the intermediate statuses during the gradual denoising generation process in DPM. The empirical observations indicate, the shape of image is reconstructed after the first few denoising steps, and then the image is filled with details (e.g., texture). The phenomenon is because the low-frequency signal (shape relevant) of the noisy image is not corrupted until the final stage in the forward process (initial stage of generation) of adding noise in DPM. Inspired by the observations, we proceed to explore the influence of each token in the text prompt during the two stages. After a series of experiments of T2I generations conditioned on a set of text prompts. We conclude that in the earlier generation stage, the image is mostly decided by the special token [\texttt{EOS}] in the text prompt, and the information in the text prompt is already conveyed in this stage. After that, the diffusion model completes the details of generated images by information from themselves. Finally, we propose to apply this observation to accelerate the process of T2I generation by properly removing text guidance, which finally accelerates the sampling up to 25\%+.

Continuous-time Riemannian SGD and SVRG Flows on Wasserstein Probabilistic Space

Recently, optimization on the Riemannian manifold has provided new insights to the optimization community. In this regard, the manifold taken as the probability measure metric space equipped with the second-order Wasserstein distance is of particular interest, since optimization on it can be linked to practical sampling processes. In general, the oracle (continuous) optimization method on Wasserstein space is Riemannian gradient flow (i.e., Langevin dynamics when minimizing KL divergence). In this paper, we aim to enrich the continuous optimization methods in the Wasserstein space by extending the gradient flow into the stochastic gradient descent (SGD) flow and stochastic variance reduction gradient (SVRG) flow. The two flows on Euclidean space are standard stochastic optimization methods, while their Riemannian counterparts are not explored yet. By leveraging the structures in Wasserstein space, we construct a stochastic differential equation (SDE) to approximate the discrete dynamics of desired stochastic methods in the corresponded random vector space. Then, the flows of probability measures are naturally obtained by applying Fokker-Planck equation to such SDE. Furthermore, the convergence rates of the proposed Riemannian stochastic flows are proven, and they match the results in Euclidean space.

SA-Solver: Stochastic Adams Solver for Fast Sampling of Diffusion Models

Diffusion Probabilistic Models (DPMs) have achieved considerable success in generation tasks. As sampling from DPMs is equivalent to solving diffusion SDE or ODE which is time-consuming, numerous fast sampling methods built upon improved differential equation solvers are proposed. The majority of such techniques consider solving the diffusion ODE due to its superior efficiency. However, stochastic sampling could offer additional advantages in generating diverse and high-quality data. In this work, we engage in a comprehensive analysis of stochastic sampling from two aspects: variance-controlled diffusion SDE and linear multi-step SDE solver. Based on our analysis, we propose SA-Solver, which is an improved efficient stochastic Adams method for solving diffusion SDE to generate data with high quality. Our experiments show that SA-Solver achieves: 1) improved or comparable performance compared with the existing state-of-the-art sampling methods for few-step sampling; 2) SOTA FID scores on substantial benchmark datasets under a suitable number of function evaluations (NFEs).

On the Generalization of Diffusion Model

The diffusion probabilistic generative models are widely used to generate high-quality data. Though they can synthetic data that does not exist in the training set, the rationale behind such generalization is still unexplored. In this paper, we formally define the generalization of the generative model, which is measured by the mutual information between the generated data and the training set. The definition originates from the intuition that the model which generates data with less correlation to the training set exhibits better generalization ability. Meanwhile, we show that for the empirical optimal diffusion model, the data generated by a deterministic sampler are all highly related to the training set, thus poor generalization. This result contradicts the observation of the trained diffusion model's (approximating empirical optima) extrapolation ability (generating unseen data). To understand this contradiction, we empirically verify the difference between the sufficiently trained diffusion model and the empirical optima. We found, though obtained through sufficient training, there still exists a slight difference between them, which is critical to making the diffusion model generalizable. Moreover, we propose another training objective whose empirical optimal solution has no potential generalization problem. We empirically show that the proposed training objective returns a similar model to the original one, which further verifies the generalization ability of the trained diffusion model.

Improved OOD Generalization via Conditional Invariant Regularizer

Recently, generalization on out-of-distribution (OOD) data with correlation shift has attracted great attention. The correlation shift is caused by the spurious attributes that correlate to the class label, as the correlation between them may vary in training and test data. For such a problem, we show that given the class label, the conditionally independent models of spurious attributes are OOD generalizable. Based on this, a metric Conditional Spurious Variation (CSV) which controls OOD generalization error, is proposed to measure such conditional independence. To improve the OOD generalization, we regularize the training process with the proposed CSV. Under mild assumptions, our training objective can be formulated as a nonconvex-concave mini-max problem. An algorithm with provable convergence rate is proposed to solve the problem. Extensive empirical results verify our algorithm's efficacy in improving OOD generalization.

Out-of-distribution Generalization with Causal Invariant Transformations

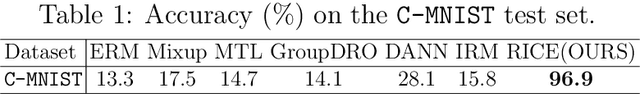
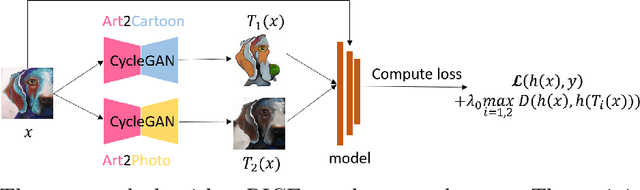
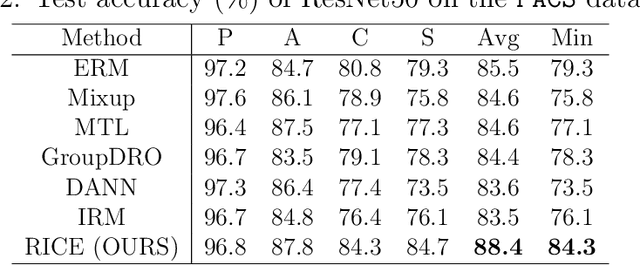
In real-world applications, it is important and desirable to learn a model that performs well on out-of-distribution (OOD) data. Recently, causality has become a powerful tool to tackle the OOD generalization problem, with the idea resting on the causal mechanism that is invariant across domains of interest. To leverage the generally unknown causal mechanism, existing works assume a linear form of causal feature or require sufficiently many and diverse training domains, which are usually restrictive in practice. In this work, we obviate these assumptions and tackle the OOD problem without explicitly recovering the causal feature. Our approach is based on transformations that modify the non-causal feature but leave the causal part unchanged, which can be either obtained from prior knowledge or learned from the training data in the multi-domain scenario. Under the setting of invariant causal mechanism, we theoretically show that if all such transformations are available, then we can learn a minimax optimal model across the domains using only single domain data. Noticing that knowing a complete set of these causal invariant transformations may be impractical, we further show that it suffices to know only a subset of these transformations. Based on the theoretical findings, a regularized training procedure is proposed to improve the OOD generalization capability. Extensive experimental results on both synthetic and real datasets verify the effectiveness of the proposed algorithm, even with only a few causal invariant transformations.

Towards the Generalization of Contrastive Self-Supervised Learning

Recently, self-supervised learning has attracted great attention since it only requires unlabeled data for training. Contrastive learning is a popular approach for self-supervised learning and empirically performs well in practice. However, the theoretical understanding of its generalization ability on downstream tasks is not well studied. To this end, we present a theoretical explanation of how contrastive self-supervised pre-trained models generalize to downstream tasks. Concretely, we quantitatively show that the self-supervised model has generalization ability on downstream classification tasks if it embeds input data into a feature space with distinguishing centers of classes and closely clustered intra-class samples. With the above conclusion, we further explore SimCLR and Barlow Twins, which are two canonical contrastive self-supervised methods. We prove that the aforementioned feature space can be obtained via any of the methods, and thus explain their success on the generalization on downstream classification tasks. Finally, various experiments are also conducted to verify our theoretical findings.

Improved OOD Generalization via Adversarial Training and Pre-training

Recently, learning a model that generalizes well on out-of-distribution (OOD) data has attracted great attention in the machine learning community. In this paper, after defining OOD generalization via Wasserstein distance, we theoretically show that a model robust to input perturbation generalizes well on OOD data. Inspired by previous findings that adversarial training helps improve input-robustness, we theoretically show that adversarially trained models have converged excess risk on OOD data, and empirically verify it on both image classification and natural language understanding tasks. Besides, in the paradigm of first pre-training and then fine-tuning, we theoretically show that a pre-trained model that is more robust to input perturbation provides a better initialization for generalization on downstream OOD data. Empirically, after fine-tuning, this better-initialized model from adversarial pre-training also has better OOD generalization.