Spatial Decompositions for Large Scale SVMs

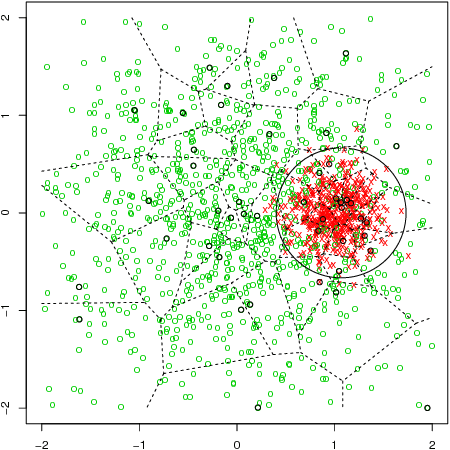
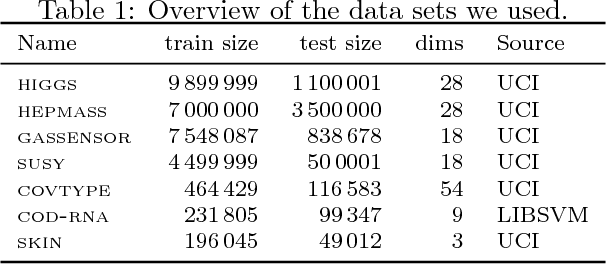
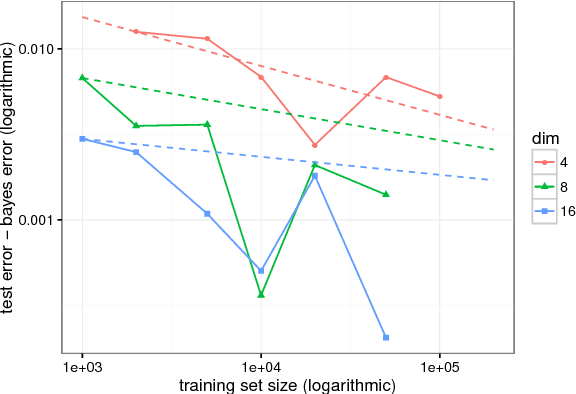
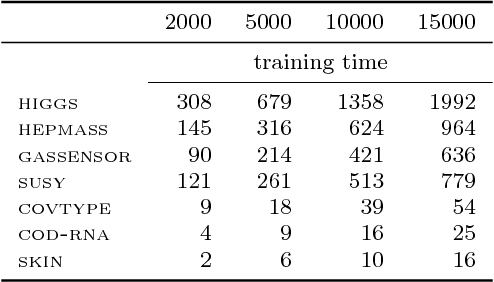
Although support vector machines (SVMs) are theoretically well understood, their underlying optimization problem becomes very expensive, if, for example, hundreds of thousands of samples and a non-linear kernel are considered. Several approaches have been proposed in the past to address this serious limitation. In this work we investigate a decomposition strategy that learns on small, spatially defined data chunks. Our contributions are two fold: On the theoretical side we establish an oracle inequality for the overall learning method using the hinge loss, and show that the resulting rates match those known for SVMs solving the complete optimization problem with Gaussian kernels. On the practical side we compare our approach to learning SVMs on small, randomly chosen chunks. Here it turns out that for comparable training times our approach is significantly faster during testing and also reduces the test error in most cases significantly. Furthermore, we show that our approach easily scales up to 10 million training samples: including hyper-parameter selection using cross validation, the entire training only takes a few hours on a single machine. Finally, we report an experiment on 32 million training samples. All experiments used liquidSVM (Steinwart and Thomann, 2017).

Adaptive Clustering Using Kernel Density Estimators

We investigate statistical properties of a clustering algorithm that receives level set estimates from a kernel density estimator and then estimates the first split in the density level cluster tree if such a split is present or detects the absence of such a split. Key aspects of our analysis include finite sample guarantees, consistency, rates of convergence, and an adaptive data-driven strategy for chosing the kernel bandwidth. For the rates and the adaptivity we do not need continuity assumptions on the density such as H\"older continuity, but only require intuitive geometric assumptions of non-parametric nature.

liquidSVM: A Fast and Versatile SVM package

liquidSVM is a package written in C++ that provides SVM-type solvers for various classification and regression tasks. Because of a fully integrated hyper-parameter selection, very carefully implemented solvers, multi-threading and GPU support, and several built-in data decomposition strategies it provides unprecedented speed for small training sizes as well as for data sets of tens of millions of samples. Besides the C++ API and a command line interface, bindings to R, MATLAB, Java, Python, and Spark are available. We present a brief description of the package and report experimental comparisons to other SVM packages.

Learning with Hierarchical Gaussian Kernels

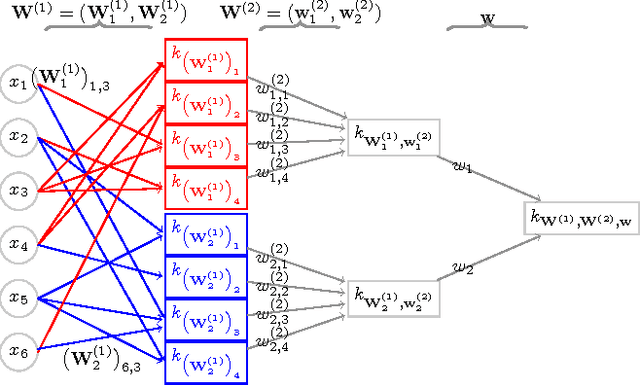
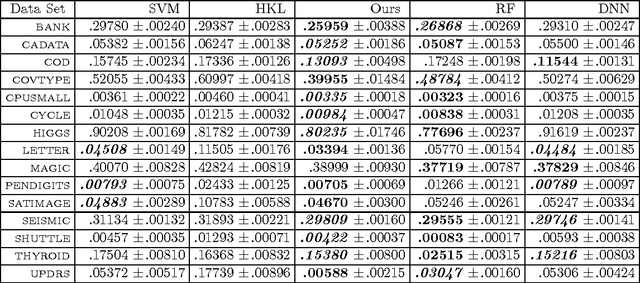
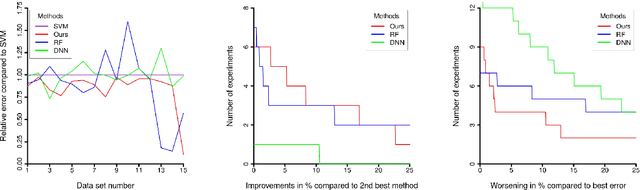
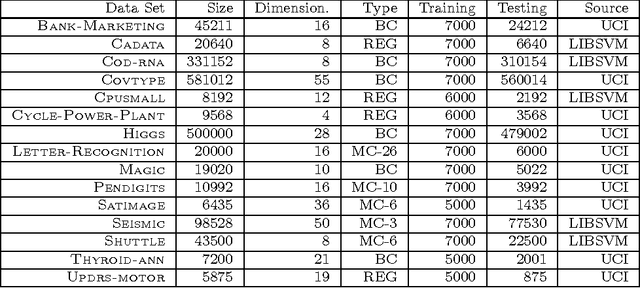
We investigate iterated compositions of weighted sums of Gaussian kernels and provide an interpretation of the construction that shows some similarities with the architectures of deep neural networks. On the theoretical side, we show that these kernels are universal and that SVMs using these kernels are universally consistent. We further describe a parameter optimization method for the kernel parameters and empirically compare this method to SVMs, random forests, a multiple kernel learning approach, and to some deep neural networks.

Towards an Axiomatic Approach to Hierarchical Clustering of Measures

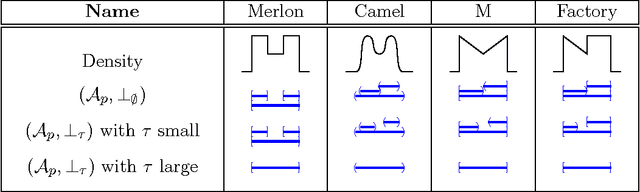
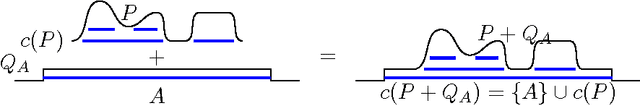
We propose some axioms for hierarchical clustering of probability measures and investigate their ramifications. The basic idea is to let the user stipulate the clusters for some elementary measures. This is done without the need of any notion of metric, similarity or dissimilarity. Our main results then show that for each suitable choice of user-defined clustering on elementary measures we obtain a unique notion of clustering on a large set of distributions satisfying a set of additivity and continuity axioms. We illustrate the developed theory by numerous examples including some with and some without a density.