Learning with Hierarchical Gaussian Kernels
Paper and Code
Dec 02, 2016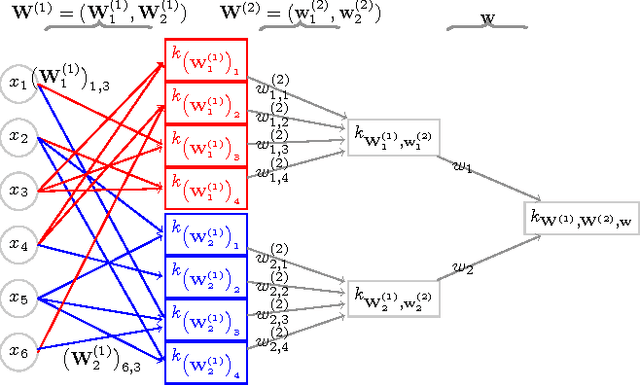
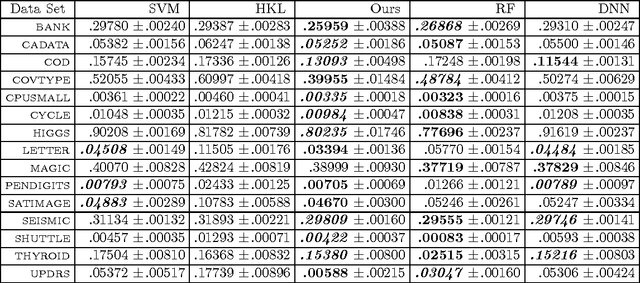
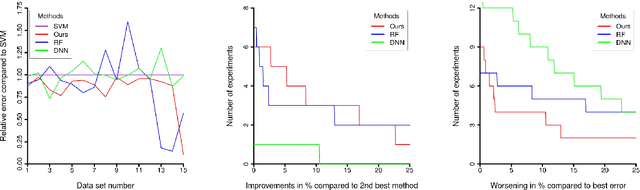
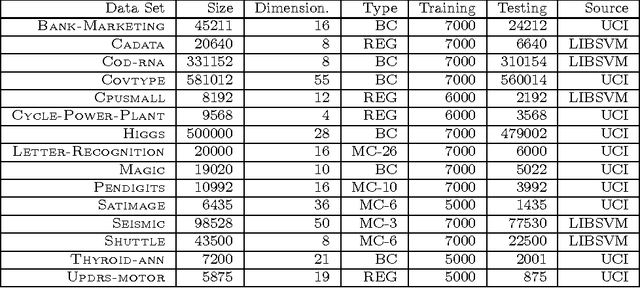
We investigate iterated compositions of weighted sums of Gaussian kernels and provide an interpretation of the construction that shows some similarities with the architectures of deep neural networks. On the theoretical side, we show that these kernels are universal and that SVMs using these kernels are universally consistent. We further describe a parameter optimization method for the kernel parameters and empirically compare this method to SVMs, random forests, a multiple kernel learning approach, and to some deep neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge