Out of Distribution Detection via Domain-Informed Gaussian Process State Space Models

In order for robots to safely navigate in unseen scenarios using learning-based methods, it is important to accurately detect out-of-training-distribution (OoD) situations online. Recently, Gaussian process state-space models (GPSSMs) have proven useful to discriminate unexpected observations by comparing them against probabilistic predictions. However, the capability for the model to correctly distinguish between in- and out-of-training distribution observations hinges on the accuracy of these predictions, primarily affected by the class of functions the GPSSM kernel can represent. In this paper, we propose (i) a novel approach to embed existing domain knowledge in the kernel and (ii) an OoD online runtime monitor, based on receding-horizon predictions. Domain knowledge is provided in the form of a dataset, collected either in simulation or by using a nominal model. Numerical results show that the informed kernel yields better regression quality with smaller datasets, as compared to standard kernel choices. We demonstrate the effectiveness of the OoD monitor on a real quadruped navigating an indoor setting, which reliably classifies previously unseen terrains.

GoSafe: Globally Optimal Safe Robot Learning

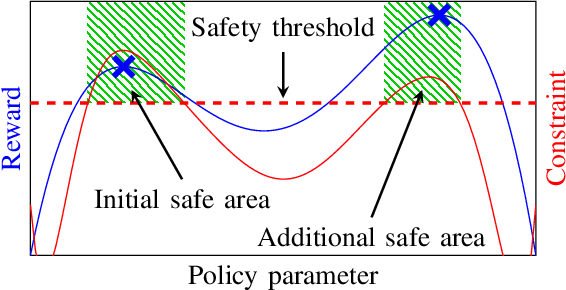
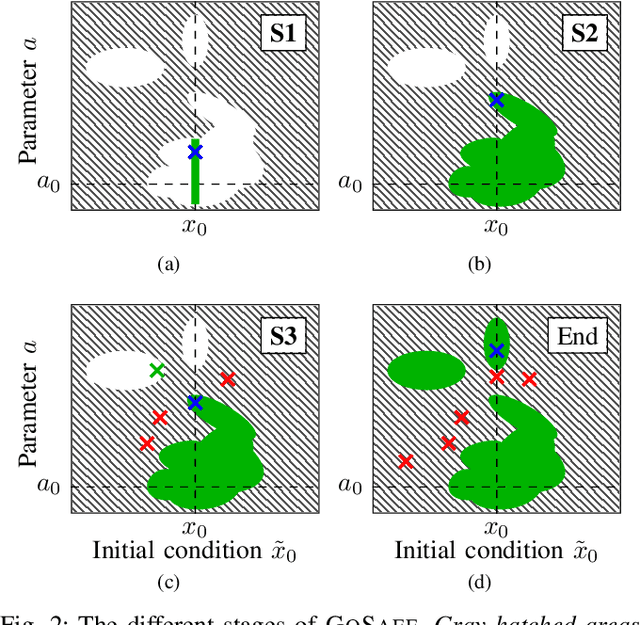
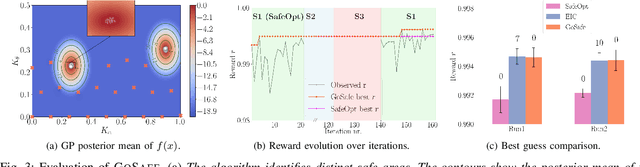
When learning policies for robotic systems from data, safety is a major concern, as violation of safety constraints may cause hardware damage. SafeOpt is an efficient Bayesian optimization (BO) algorithm that can learn policies while guaranteeing safety with high probability. However, its search space is limited to an initially given safe region. We extend this method by exploring outside the initial safe area while still guaranteeing safety with high probability. This is achieved by learning a set of initial conditions from which we can recover safely using a learned backup controller in case of a potential failure. We derive conditions for guaranteed convergence to the global optimum and validate GoSafe in hardware experiments.

Robot Learning with Crash Constraints

In the past decade, numerous machine learning algorithms have been shown to successfully learn optimal policies to control real robotic systems. However, it is not rare to encounter failing behaviors as the learning loop progresses. Specifically, in robot applications where failing is undesired but not catastrophic, many algorithms struggle with leveraging data obtained from failures. This is usually caused by (i) the failed experiment ending prematurely, or (ii) the acquired data being scarce or corrupted. Both complicate the design of proper reward functions to penalize failures. In this paper, we propose a framework that addresses those issues. We consider failing behaviors as those that violate a constraint and address the problem of "learning with crash constraints", where no data is obtained upon constraint violation. The no-data case is addressed by a novel GP model (GPCR) for the constraint that combines discrete events (failure/success) with continuous observations (only obtained upon success). We demonstrate the effectiveness of our framework on simulated benchmarks and on a real jumping quadruped, where the constraint boundary is unknown a priori. Experimental data is collected, by means of constrained Bayesian optimization, directly on the real robot. Our results outperform manual tuning and GPCR proves useful on estimating the constraint boundary.

Excursion Search for Constrained Bayesian Optimization under a Limited Budget of Failures

When learning to ride a bike, a child falls down a number of times before achieving the first success. As falling down usually has only mild consequences, it can be seen as a tolerable failure in exchange for a faster learning process, as it provides rich information about an undesired behavior. In the context of Bayesian optimization under unknown constraints (BOC), typical strategies for safe learning explore conservatively and avoid failures by all means. On the other side of the spectrum, non conservative BOC algorithms that allow failing may fail an unbounded number of times before reaching the optimum. In this work, we propose a novel decision maker grounded in control theory that controls the amount of risk we allow in the search as a function of a given budget of failures. Empirical validation shows that our algorithm uses the failures budget more efficiently in a variety of optimization experiments, and generally achieves lower regret, than state-of-the-art methods. In addition, we propose an original algorithm for unconstrained Bayesian optimization inspired by the notion of excursion sets in stochastic processes, upon which the failures-aware algorithm is built.

Classified Regression for Bayesian Optimization: Robot Learning with Unknown Penalties

Learning robot controllers by minimizing a black-box objective cost using Bayesian optimization (BO) can be time-consuming and challenging. It is very often the case that some roll-outs result in failure behaviors, causing premature experiment detention. In such cases, the designer is forced to decide on heuristic cost penalties because the acquired data is often scarce, or not comparable with that of the stable policies. To overcome this, we propose a Bayesian model that captures exactly what we know about the cost of unstable controllers prior to data collection: Nothing, except that it should be a somewhat large number. The resulting Bayesian model, approximated with a Gaussian process, predicts high cost values in regions where failures are likely to occur. In this way, the model guides the BO exploration toward regions of stability. We demonstrate the benefits of the proposed model in several illustrative and statistical synthetic benchmarks, and also in experiments on a real robotic platform. In addition, we propose and experimentally validate a new BO method to account for unknown constraints. Such method is an extension of Max-Value Entropy Search, a recent information-theoretic method, to solve unconstrained global optimization problems.

Data-efficient Auto-tuning with Bayesian Optimization: An Industrial Control Study

Bayesian optimization is proposed for automatic learning of optimal controller parameters from experimental data. A probabilistic description (a Gaussian process) is used to model the unknown function from controller parameters to a user-defined cost. The probabilistic model is updated with data, which is obtained by testing a set of parameters on the physical system and evaluating the cost. In order to learn fast, the Bayesian optimization algorithm selects the next parameters to evaluate in a systematic way, for example, by maximizing information gain about the optimum. The algorithm thus iteratively finds the globally optimal parameters with only few experiments. Taking throttle valve control as a representative industrial control example, the proposed auto-tuning method is shown to outperform manual calibration: it consistently achieves better performance with a low number of experiments. The proposed auto-tuning framework is flexible and can handle different control structures and objectives.

Gait learning for soft microrobots controlled by light fields

Soft microrobots based on photoresponsive materials and controlled by light fields can generate a variety of different gaits. This inherent flexibility can be exploited to maximize their locomotion performance in a given environment and used to adapt them to changing conditions. Albeit, because of the lack of accurate locomotion models, and given the intrinsic variability among microrobots, analytical control design is not possible. Common data-driven approaches, on the other hand, require running prohibitive numbers of experiments and lead to very sample-specific results. Here we propose a probabilistic learning approach for light-controlled soft microrobots based on Bayesian Optimization (BO) and Gaussian Processes (GPs). The proposed approach results in a learning scheme that is data-efficient, enabling gait optimization with a limited experimental budget, and robust against differences among microrobot samples. These features are obtained by designing the learning scheme through the comparison of different GP priors and BO settings on a semi-synthetic data set. The developed learning scheme is validated in microrobot experiments, resulting in a 115% improvement in a microrobot's locomotion performance with an experimental budget of only 20 tests. These encouraging results lead the way toward self-adaptive microrobotic systems based on light-controlled soft microrobots and probabilistic learning control.

On the Design of LQR Kernels for Efficient Controller Learning

Finding optimal feedback controllers for nonlinear dynamic systems from data is hard. Recently, Bayesian optimization (BO) has been proposed as a powerful framework for direct controller tuning from experimental trials. For selecting the next query point and finding the global optimum, BO relies on a probabilistic description of the latent objective function, typically a Gaussian process (GP). As is shown herein, GPs with a common kernel choice can, however, lead to poor learning outcomes on standard quadratic control problems. For a first-order system, we construct two kernels that specifically leverage the structure of the well-known Linear Quadratic Regulator (LQR), yet retain the flexibility of Bayesian nonparametric learning. Simulations of uncertain linear and nonlinear systems demonstrate that the LQR kernels yield superior learning performance.

Model-Based Policy Search for Automatic Tuning of Multivariate PID Controllers

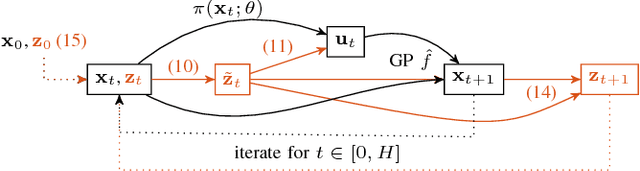
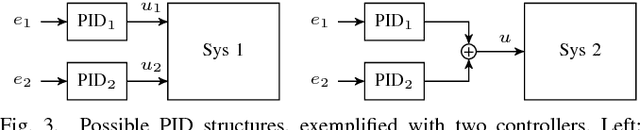
PID control architectures are widely used in industrial applications. Despite their low number of open parameters, tuning multiple, coupled PID controllers can become tedious in practice. In this paper, we extend PILCO, a model-based policy search framework, to automatically tune multivariate PID controllers purely based on data observed on an otherwise unknown system. The system's state is extended appropriately to frame the PID policy as a static state feedback policy. This renders PID tuning possible as the solution of a finite horizon optimal control problem without further a priori knowledge. The framework is applied to the task of balancing an inverted pendulum on a seven degree-of-freedom robotic arm, thereby demonstrating its capabilities of fast and data-efficient policy learning, even on complex real world problems.

Virtual vs. Real: Trading Off Simulations and Physical Experiments in Reinforcement Learning with Bayesian Optimization

In practice, the parameters of control policies are often tuned manually. This is time-consuming and frustrating. Reinforcement learning is a promising alternative that aims to automate this process, yet often requires too many experiments to be practical. In this paper, we propose a solution to this problem by exploiting prior knowledge from simulations, which are readily available for most robotic platforms. Specifically, we extend Entropy Search, a Bayesian optimization algorithm that maximizes information gain from each experiment, to the case of multiple information sources. The result is a principled way to automatically combine cheap, but inaccurate information from simulations with expensive and accurate physical experiments in a cost-effective manner. We apply the resulting method to a cart-pole system, which confirms that the algorithm can find good control policies with fewer experiments than standard Bayesian optimization on the physical system only.