Topological obstruction to the training of shallow ReLU neural networks

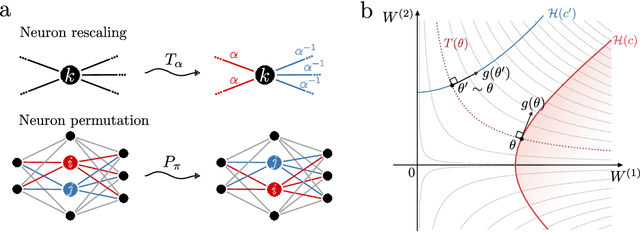
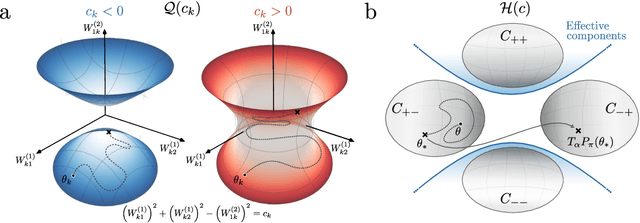
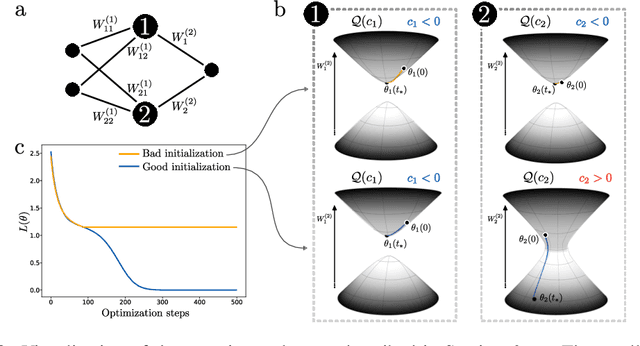
Studying the interplay between the geometry of the loss landscape and the optimization trajectories of simple neural networks is a fundamental step for understanding their behavior in more complex settings. This paper reveals the presence of topological obstruction in the loss landscape of shallow ReLU neural networks trained using gradient flow. We discuss how the homogeneous nature of the ReLU activation function constrains the training trajectories to lie on a product of quadric hypersurfaces whose shape depends on the particular initialization of the network's parameters. When the neural network's output is a single scalar, we prove that these quadrics can have multiple connected components, limiting the set of reachable parameters during training. We analytically compute the number of these components and discuss the possibility of mapping one to the other through neuron rescaling and permutation. In this simple setting, we find that the non-connectedness results in a topological obstruction, which, depending on the initialization, can make the global optimum unreachable. We validate this result with numerical experiments.