Optimizing Sequential Experimental Design with Deep Reinforcement Learning
Paper and Code
Feb 02, 2022
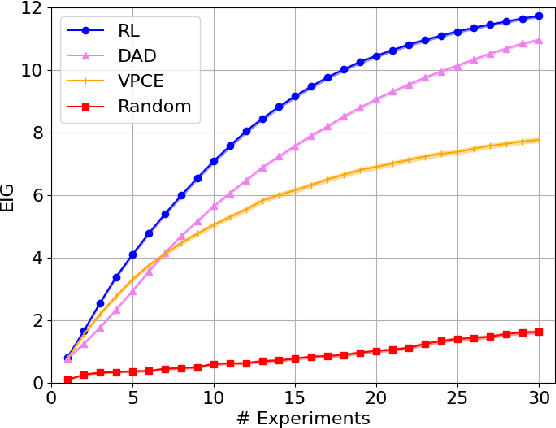
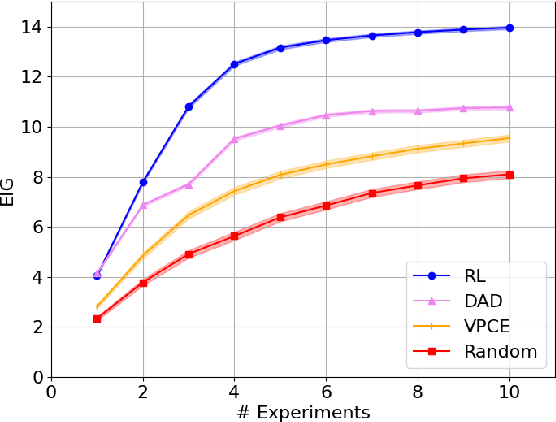
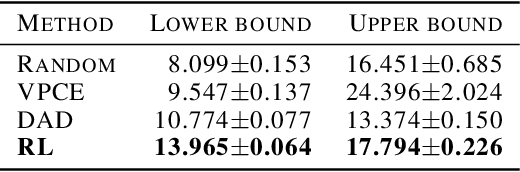
Bayesian approaches developed to solve the optimal design of sequential experiments are mathematically elegant but computationally challenging. Recently, techniques using amortization have been proposed to make these Bayesian approaches practical, by training a parameterized policy that proposes designs efficiently at deployment time. However, these methods may not sufficiently explore the design space, require access to a differentiable probabilistic model and can only optimize over continuous design spaces. Here, we address these limitations by showing that the problem of optimizing policies can be reduced to solving a Markov decision process (MDP). We solve the equivalent MDP with modern deep reinforcement learning techniques. Our experiments show that our approach is also computationally efficient at deployment time and exhibits state-of-the-art performance on both continuous and discrete design spaces, even when the probabilistic model is a black box.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge