Approximate Nearest Neighbour Search on Dynamic Datasets: An Investigation

Approximate k-Nearest Neighbour (ANN) methods are often used for mining information and aiding machine learning on large scale high-dimensional datasets. ANN methods typically differ in the index structure used for accelerating searches, resulting in various recall/runtime trade-off points. For applications with static datasets, runtime constraints and dataset properties can be used to empirically select an ANN method with suitable operating characteristics. However, for applications with dynamic datasets, which are subject to frequent online changes (like addition of new samples), there is currently no consensus as to which ANN methods are most suitable. Traditional evaluation approaches do not consider the computational costs of updating the index structure, as well as the frequency and size of index updates. To address this, we empirically evaluate 5 popular ANN methods on two main applications (online data collection and online feature learning) while taking into account these considerations. Two dynamic datasets are used, derived from the SIFT1M dataset with 1 million samples and the DEEP1B dataset with 1 billion samples. The results indicate that the often used k-d trees method is not suitable on dynamic datasets as it is slower than a straightforward baseline exhaustive search method. For online data collection, the Hierarchical Navigable Small World Graphs method achieves a consistent speedup over baseline across a wide range of recall rates. For online feature learning, the Scalable Nearest Neighbours method is faster than baseline for recall rates below 75%.

Cross-Entropy Estimators for Sequential Experiment Design with Reinforcement Learning

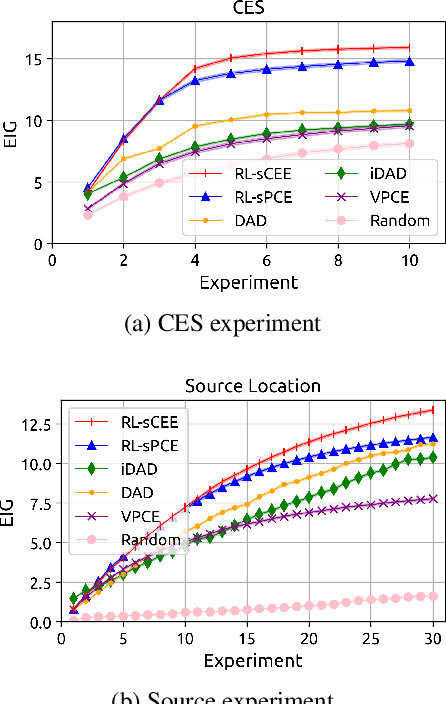
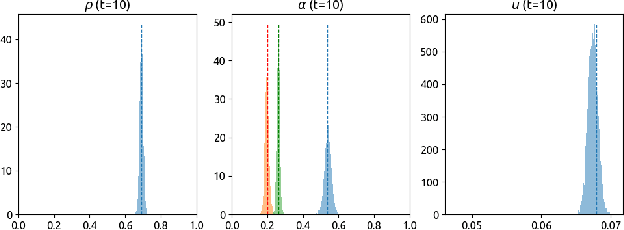
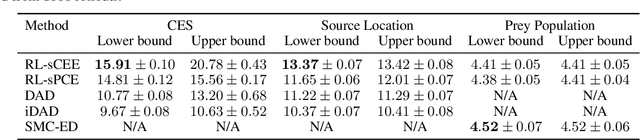
Reinforcement learning can effectively learn amortised design policies for designing sequences of experiments. However, current methods rely on contrastive estimators of expected information gain, which require an exponential number of contrastive samples to achieve an unbiased estimation. We propose an alternative lower bound estimator, based on the cross-entropy of the joint model distribution and a flexible proposal distribution. This proposal distribution approximates the true posterior of the model parameters given the experimental history and the design policy. Our estimator requires no contrastive samples, can achieve more accurate estimates of high information gains, allows learning of superior design policies, and is compatible with implicit probabilistic models. We assess our algorithm's performance in various tasks, including continuous and discrete designs and explicit and implicit likelihoods.

Bayesian Optimisation for Mixed-Variable Inputs using Value Proposals

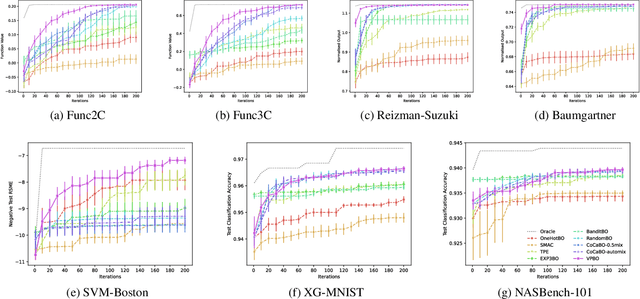
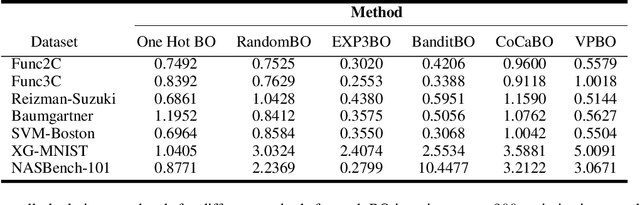
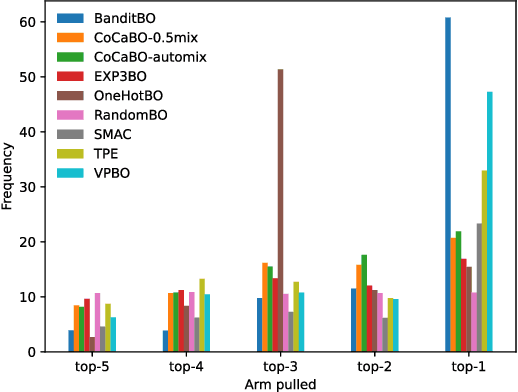
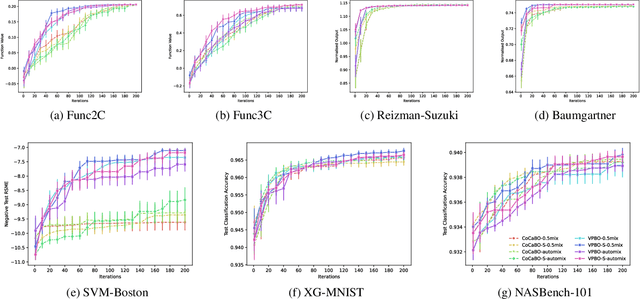
Many real-world optimisation problems are defined over both categorical and continuous variables, yet efficient optimisation methods such asBayesian Optimisation (BO) are not designed tohandle such mixed-variable search spaces. Recent approaches to this problem cast the selection of the categorical variables as a bandit problem, operating independently alongside a BO component which optimises the continuous variables. In this paper, we adopt a holistic view and aim to consolidate optimisation of the categorical and continuous sub-spaces under a single acquisition metric. We derive candidates from the ExpectedImprovement criterion, which we call value proposals, and use these proposals to make selections on both the categorical and continuous components of the input. We show that this unified approach significantly outperforms existing mixed-variable optimisation approaches across several mixed-variable black-box optimisation tasks.

Optimizing Sequential Experimental Design with Deep Reinforcement Learning

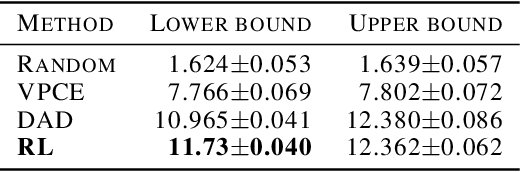
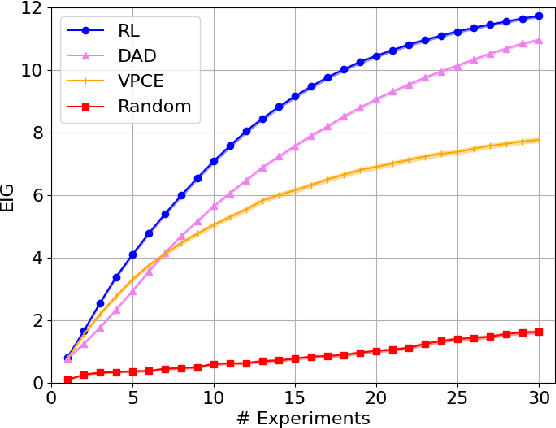
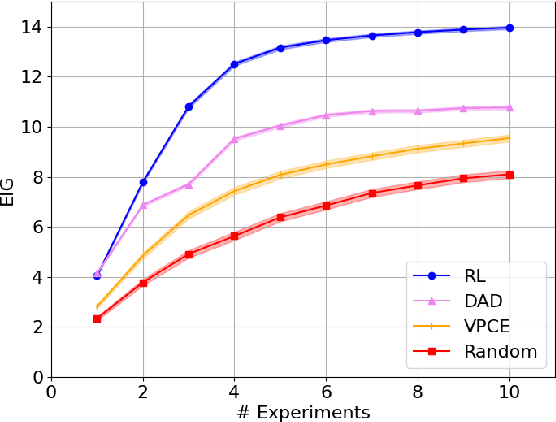
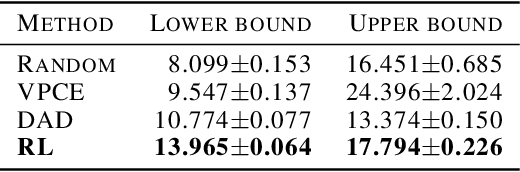
Bayesian approaches developed to solve the optimal design of sequential experiments are mathematically elegant but computationally challenging. Recently, techniques using amortization have been proposed to make these Bayesian approaches practical, by training a parameterized policy that proposes designs efficiently at deployment time. However, these methods may not sufficiently explore the design space, require access to a differentiable probabilistic model and can only optimize over continuous design spaces. Here, we address these limitations by showing that the problem of optimizing policies can be reduced to solving a Markov decision process (MDP). We solve the equivalent MDP with modern deep reinforcement learning techniques. Our experiments show that our approach is also computationally efficient at deployment time and exhibits state-of-the-art performance on both continuous and discrete design spaces, even when the probabilistic model is a black box.