An Overview of Causal Inference using Kernel Embeddings
Paper and Code
Oct 30, 2024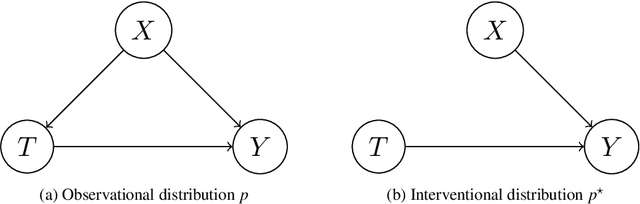
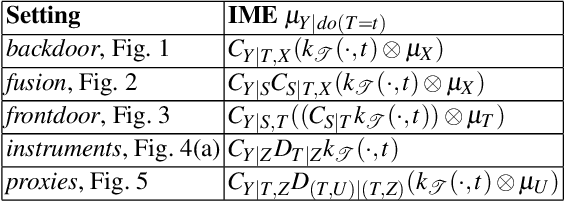
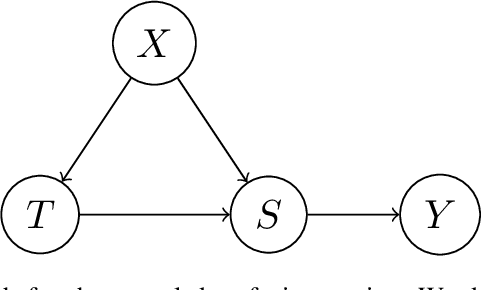
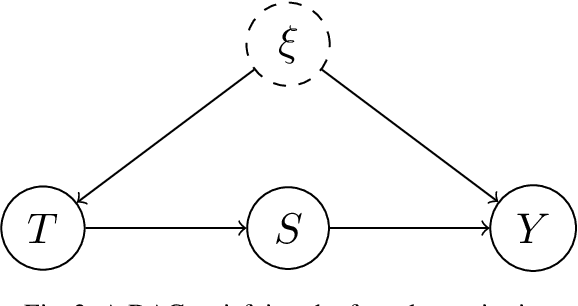
Kernel embeddings have emerged as a powerful tool for representing probability measures in a variety of statistical inference problems. By mapping probability measures into a reproducing kernel Hilbert space (RKHS), kernel embeddings enable flexible representations of complex relationships between variables. They serve as a mechanism for efficiently transferring the representation of a distribution downstream to other tasks, such as hypothesis testing or causal effect estimation. In the context of causal inference, the main challenges include identifying causal associations and estimating the average treatment effect from observational data, where confounding variables may obscure direct cause-and-effect relationships. Kernel embeddings provide a robust nonparametric framework for addressing these challenges. They allow for the representations of distributions of observational data and their seamless transformation into representations of interventional distributions to estimate relevant causal quantities. We overview recent research that leverages the expressiveness of kernel embeddings in tandem with causal inference.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge