Heterogeneous Treatment Effect in Time-to-Event Outcomes: Harnessing Censored Data with Recursively Imputed Trees

Tailoring treatments to individual needs is a central goal in fields such as medicine. A key step toward this goal is estimating Heterogeneous Treatment Effects (HTE) - the way treatments impact different subgroups. While crucial, HTE estimation is challenging with survival data, where time until an event (e.g., death) is key. Existing methods often assume complete observation, an assumption violated in survival data due to right-censoring, leading to bias and inefficiency. Cui et al. (2023) proposed a doubly-robust method for HTE estimation in survival data under no hidden confounders, combining a causal survival forest with an augmented inverse-censoring weighting estimator. However, we find it struggles under heavy censoring, which is common in rare-outcome problems such as Amyotrophic lateral sclerosis (ALS). Moreover, most current methods cannot handle instrumental variables, which are a crucial tool in the causal inference arsenal. We introduce Multiple Imputation for Survival Treatment Response (MISTR), a novel, general, and non-parametric method for estimating HTE in survival data. MISTR uses recursively imputed survival trees to handle censoring without directly modeling the censoring mechanism. Through extensive simulations and analysis of two real-world datasets-the AIDS Clinical Trials Group Protocol 175 and the Illinois unemployment dataset we show that MISTR outperforms prior methods under heavy censoring in the no-hidden-confounders setting, and extends to the instrumental variable setting. To our knowledge, MISTR is the first non-parametric approach for HTE estimation with unobserved confounders via instrumental variables.

Confidence Intervals and Simultaneous Confidence Bands Based on Deep Learning

Deep learning models have significantly improved prediction accuracy in various fields, gaining recognition across numerous disciplines. Yet, an aspect of deep learning that remains insufficiently addressed is the assessment of prediction uncertainty. Producing reliable uncertainty estimators could be crucial in practical terms. For instance, predictions associated with a high degree of uncertainty could be sent for further evaluation. Recent works in uncertainty quantification of deep learning predictions, including Bayesian posterior credible intervals and a frequentist confidence-interval estimation, have proven to yield either invalid or overly conservative intervals. Furthermore, there is currently no method for quantifying uncertainty that can accommodate deep neural networks for survival (time-to-event) data that involves right-censored outcomes. In this work, we provide a valid non-parametric bootstrap method that correctly disentangles data uncertainty from the noise inherent in the adopted optimization algorithm, ensuring that the resulting point-wise confidence intervals or the simultaneous confidence bands are accurate (i.e., valid and not overly conservative). The proposed ad-hoc method can be easily integrated into any deep neural network without interfering with the training process. The utility of the proposed approach is illustrated by constructing simultaneous confidence bands for survival curves derived from deep neural networks for survival data with right censoring.

Discrete-time Competing-Risks Regression with or without Penalization

Many studies employ the analysis of time-to-event data that incorporates competing risks and right censoring. Most methods and software packages are geared towards analyzing data that comes from a continuous failure time distribution. However, failure-time data may sometimes be discrete either because time is inherently discrete or due to imprecise measurement. This paper introduces a novel estimation procedure for discrete-time survival analysis with competing events. The proposed approach offers two key advantages over existing procedures: first, it accelerates the estimation process; second, it allows for straightforward integration and application of widely used regularized regression and screening methods. We illustrate the benefits of our proposed approach by conducting a comprehensive simulation study. Additionally, we showcase the utility of our procedure by estimating a survival model for the length of stay of patients hospitalized in the intensive care unit, considering three competing events: discharge to home, transfer to another medical facility, and in-hospital death.

PyDTS: A Python Package for Discrete Time Survival Analysis with Competing Risks

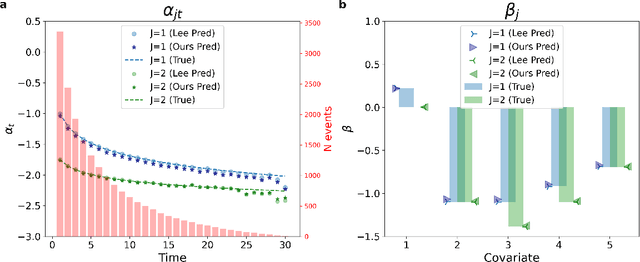
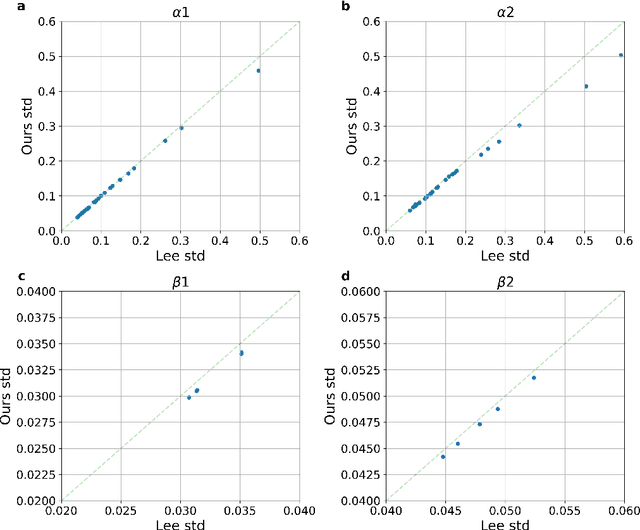
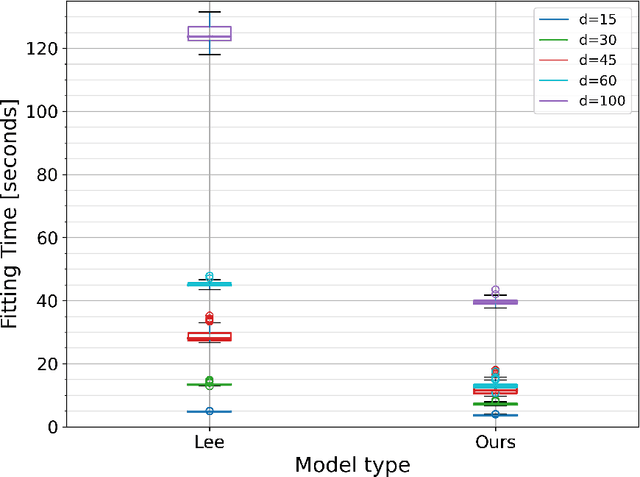
Time-to-event analysis (survival analysis) is used when the outcome or the response of interest is the time until a pre-specified event occurs. Time-to-event data are sometimes discrete either because time itself is discrete or due to grouping of failure times into intervals or rounding off measurements. In addition, the failure of an individual could be one of several distinct failure types; known as competing risks (events) data. This work focuses on discrete-time regression with competing events. We emphasize the main difference between the continuous and discrete settings with competing events, develop a new estimation procedure, and present PyDTS, an open source Python package which implements our estimation procedure and other tools for discrete-time-survival analysis with competing risks.