Benign overfitting in Fixed Dimension via Physics-Informed Learning with Smooth Inductive Bias

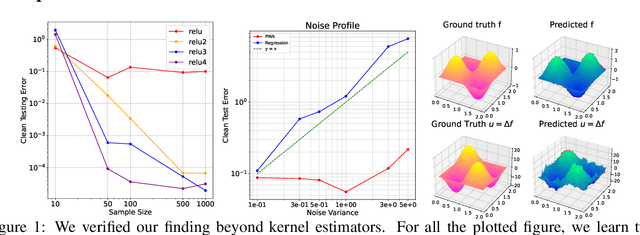
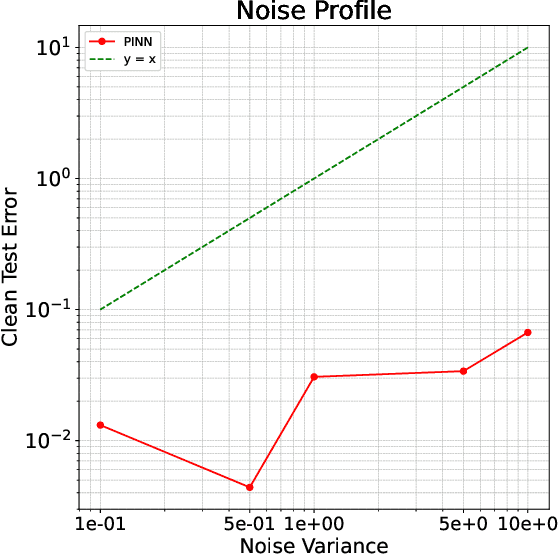
Recent advances in machine learning have inspired a surge of research into reconstructing specific quantities of interest from measurements that comply with certain physical laws. These efforts focus on inverse problems that are governed by partial differential equations (PDEs). In this work, we develop an asymptotic Sobolev norm learning curve for kernel ridge(less) regression when addressing (elliptical) linear inverse problems. Our results show that the PDE operators in the inverse problem can stabilize the variance and even behave benign overfitting for fixed-dimensional problems, exhibiting different behaviors from regression problems. Besides, our investigation also demonstrates the impact of various inductive biases introduced by minimizing different Sobolev norms as a form of implicit regularization. For the regularized least squares estimator, we find that all considered inductive biases can achieve the optimal convergence rate, provided the regularization parameter is appropriately chosen. The convergence rate is actually independent to the choice of (smooth enough) inductive bias for both ridge and ridgeless regression. Surprisingly, our smoothness requirement recovered the condition found in Bayesian setting and extend the conclusion to the minimum norm interpolation estimators.