Leello Dadi
Could ChatGPT get an Engineering Degree? Evaluating Higher Education Vulnerability to AI Assistants
Aug 07, 2024
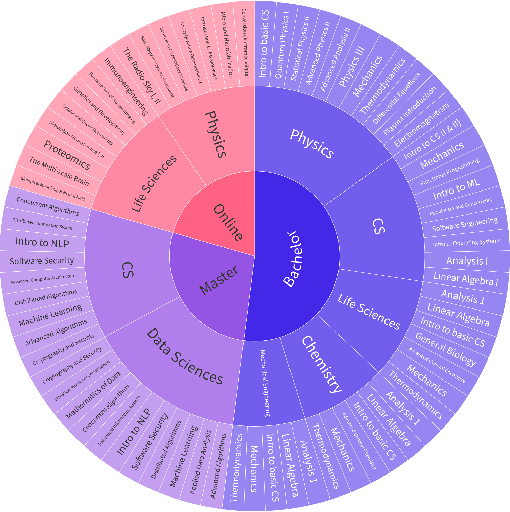
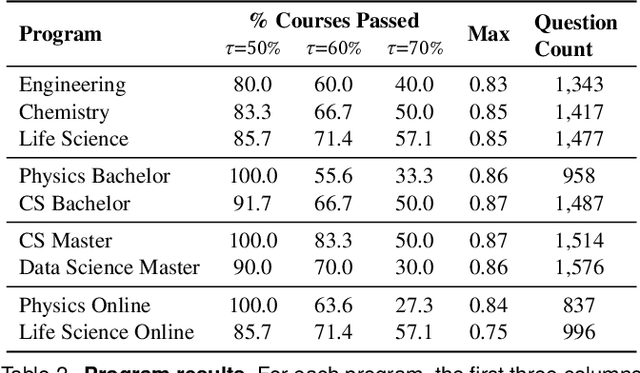

Abstract:AI assistants are being increasingly used by students enrolled in higher education institutions. While these tools provide opportunities for improved teaching and education, they also pose significant challenges for assessment and learning outcomes. We conceptualize these challenges through the lens of vulnerability, the potential for university assessments and learning outcomes to be impacted by student use of generative AI. We investigate the potential scale of this vulnerability by measuring the degree to which AI assistants can complete assessment questions in standard university-level STEM courses. Specifically, we compile a novel dataset of textual assessment questions from 50 courses at EPFL and evaluate whether two AI assistants, GPT-3.5 and GPT-4 can adequately answer these questions. We use eight prompting strategies to produce responses and find that GPT-4 answers an average of 65.8% of questions correctly, and can even produce the correct answer across at least one prompting strategy for 85.1% of questions. When grouping courses in our dataset by degree program, these systems already pass non-project assessments of large numbers of core courses in various degree programs, posing risks to higher education accreditation that will be amplified as these models improve. Our results call for revising program-level assessment design in higher education in light of advances in generative AI.
Learning with Norm Constrained, Over-parameterized, Two-layer Neural Networks
Apr 29, 2024Abstract:Recent studies show that a reproducing kernel Hilbert space (RKHS) is not a suitable space to model functions by neural networks as the curse of dimensionality (CoD) cannot be evaded when trying to approximate even a single ReLU neuron (Bach, 2017). In this paper, we study a suitable function space for over-parameterized two-layer neural networks with bounded norms (e.g., the path norm, the Barron norm) in the perspective of sample complexity and generalization properties. First, we show that the path norm (as well as the Barron norm) is able to obtain width-independence sample complexity bounds, which allows for uniform convergence guarantees. Based on this result, we derive the improved result of metric entropy for $\epsilon$-covering up to $\mathcal{O}(\epsilon^{-\frac{2d}{d+2}})$ ($d$ is the input dimension and the depending constant is at most polynomial order of $d$) via the convex hull technique, which demonstrates the separation with kernel methods with $\Omega(\epsilon^{-d})$ to learn the target function in a Barron space. Second, this metric entropy result allows for building a sharper generalization bound under a general moment hypothesis setting, achieving the rate at $\mathcal{O}(n^{-\frac{d+2}{2d+2}})$. Our analysis is novel in that it offers a sharper and refined estimation for metric entropy (with a clear dependence relationship on the dimension $d$) and unbounded sampling in the estimation of the sample error and the output error.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge