Ling Liang
OptimAI: Optimization from Natural Language Using LLM-Powered AI Agents
Apr 23, 2025



Abstract:Optimization plays a vital role in scientific research and practical applications, but formulating a concrete optimization problem described in natural language into a mathematical form and selecting a suitable solver to solve the problem requires substantial domain expertise. We introduce \textbf{OptimAI}, a framework for solving \underline{Optim}ization problems described in natural language by leveraging LLM-powered \underline{AI} agents, achieving superior performance over current state-of-the-art methods. Our framework is built upon four key roles: (1) a \emph{formulator} that translates natural language problem descriptions into precise mathematical formulations; (2) a \emph{planner} that constructs a high-level solution strategy prior to execution; and (3) a \emph{coder} and a \emph{code critic} capable of interacting with the environment and reflecting on outcomes to refine future actions. Ablation studies confirm that all roles are essential; removing the planner or code critic results in $5.8\times$ and $3.1\times$ drops in productivity, respectively. Furthermore, we introduce UCB-based debug scheduling to dynamically switch between alternative plans, yielding an additional $3.3\times$ productivity gain. Our design emphasizes multi-agent collaboration, allowing us to conveniently explore the synergistic effect of combining diverse models within a unified system. Our approach attains 88.1\% accuracy on the NLP4LP dataset and 71.2\% on the Optibench (non-linear w/o table) subset, reducing error rates by 58\% and 50\% respectively over prior best results.
HybriMoE: Hybrid CPU-GPU Scheduling and Cache Management for Efficient MoE Inference
Apr 08, 2025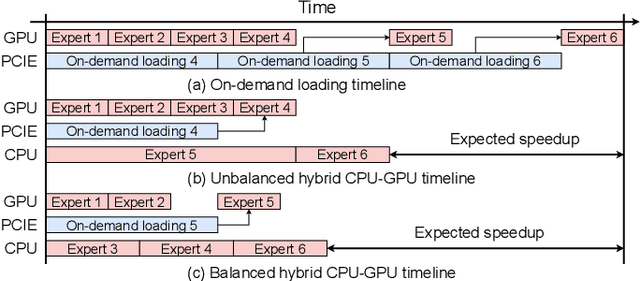
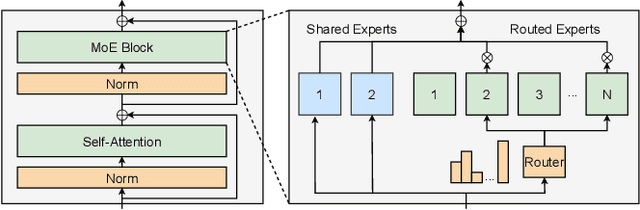
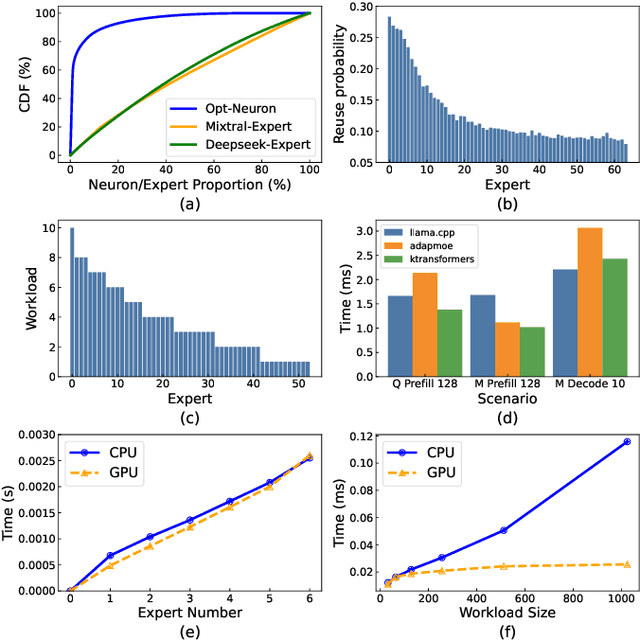
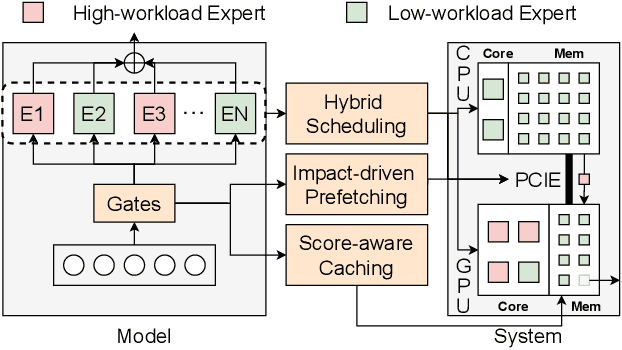
Abstract:The Mixture of Experts (MoE) architecture has demonstrated significant advantages as it enables to increase the model capacity without a proportional increase in computation. However, the large MoE model size still introduces substantial memory demands, which usually requires expert offloading on resource-constrained platforms and incurs significant overhead. Hybrid CPU-GPU inference has been proposed to leverage CPU computation to reduce expert loading overhead but faces major challenges: on one hand, the expert activation patterns of MoE models are highly unstable, rendering the fixed mapping strategies in existing works inefficient; on the other hand, the hybrid CPU-GPU schedule for MoE is inherently complex due to the diverse expert sizes, structures, uneven workload distribution, etc. To address these challenges, in this paper, we propose HybriMoE, a hybrid CPU-GPU inference framework that improves resource utilization through a novel CPU-GPU scheduling and cache management system. HybriMoE introduces (i) a dynamic intra-layer scheduling strategy to balance workloads across CPU and GPU, (ii) an impact-driven inter-layer prefetching algorithm, and (iii) a score-based caching algorithm to mitigate expert activation instability. We implement HybriMoE on top of the kTransformers framework and evaluate it on three widely used MoE-based LLMs. Experimental results demonstrate that HybriMoE achieves an average speedup of 1.33$\times$ in the prefill stage and 1.70$\times$ in the decode stage compared to state-of-the-art hybrid MoE inference framework. Our code is available at: https://github.com/PKU-SEC-Lab/HybriMoE.
From Equations to Insights: Unraveling Symbolic Structures in PDEs with LLMs
Mar 13, 2025Abstract:Motivated by the remarkable success of artificial intelligence (AI) across diverse fields, the application of AI to solve scientific problems-often formulated as partial differential equations (PDEs)-has garnered increasing attention. While most existing research concentrates on theoretical properties (such as well-posedness, regularity, and continuity) of the solutions, alongside direct AI-driven methods for solving PDEs, the challenge of uncovering symbolic relationships within these equations remains largely unexplored. In this paper, we propose leveraging large language models (LLMs) to learn such symbolic relationships. Our results demonstrate that LLMs can effectively predict the operators involved in PDE solutions by utilizing the symbolic information in the PDEs. Furthermore, we show that discovering these symbolic relationships can substantially improve both the efficiency and accuracy of the finite expression method for finding analytical approximation of PDE solutions, delivering a fully interpretable solution pipeline. This work opens new avenues for understanding the symbolic structure of scientific problems and advancing their solution processes.
Towards Effective and Sparse Adversarial Attack on Spiking Neural Networks via Breaking Invisible Surrogate Gradients
Mar 05, 2025Abstract:Spiking neural networks (SNNs) have shown their competence in handling spatial-temporal event-based data with low energy consumption. Similar to conventional artificial neural networks (ANNs), SNNs are also vulnerable to gradient-based adversarial attacks, wherein gradients are calculated by spatial-temporal back-propagation (STBP) and surrogate gradients (SGs). However, the SGs may be invisible for an inference-only model as they do not influence the inference results, and current gradient-based attacks are ineffective for binary dynamic images captured by the dynamic vision sensor (DVS). While some approaches addressed the issue of invisible SGs through universal SGs, their SGs lack a correlation with the victim model, resulting in sub-optimal performance. Moreover, the imperceptibility of existing SNN-based binary attacks is still insufficient. In this paper, we introduce an innovative potential-dependent surrogate gradient (PDSG) method to establish a robust connection between the SG and the model, thereby enhancing the adaptability of adversarial attacks across various models with invisible SGs. Additionally, we propose the sparse dynamic attack (SDA) to effectively attack binary dynamic images. Utilizing a generation-reduction paradigm, SDA can fully optimize the sparsity of adversarial perturbations. Experimental results demonstrate that our PDSG and SDA outperform state-of-the-art SNN-based attacks across various models and datasets. Specifically, our PDSG achieves 100% attack success rate on ImageNet, and our SDA obtains 82% attack success rate by modifying only 0.24% of the pixels on CIFAR10DVS. The code is available at https://github.com/ryime/PDSG-SDA .
PINS: Proximal Iterations with Sparse Newton and Sinkhorn for Optimal Transport
Feb 06, 2025



Abstract:Optimal transport (OT) is a critical problem in optimization and machine learning, where accuracy and efficiency are paramount. Although entropic regularization and the Sinkhorn algorithm improve scalability, they frequently encounter numerical instability and slow convergence, especially when the regularization parameter is small. In this work, we introduce Proximal Iterations with Sparse Newton and Sinkhorn methods (PINS) to efficiently compute highly accurate solutions for large-scale OT problems. A reduced computational complexity through overall sparsity and global convergence are guaranteed by rigorous theoretical analysis. Our approach offers three key advantages: it achieves accuracy comparable to exact solutions, progressively accelerates each iteration for greater efficiency, and enhances robustness by reducing sensitivity to regularization parameters. Extensive experiments confirm these advantages, demonstrating superior performance compared to related methods.
CopyLens: Dynamically Flagging Copyrighted Sub-Dataset Contributions to LLM Outputs
Oct 06, 2024



Abstract:Large Language Models (LLMs) have become pervasive due to their knowledge absorption and text-generation capabilities. Concurrently, the copyright issue for pretraining datasets has been a pressing concern, particularly when generation includes specific styles. Previous methods either focus on the defense of identical copyrighted outputs or find interpretability by individual tokens with computational burdens. However, the gap between them exists, where direct assessments of how dataset contributions impact LLM outputs are missing. Once the model providers ensure copyright protection for data holders, a more mature LLM community can be established. To address these limitations, we introduce CopyLens, a new framework to analyze how copyrighted datasets may influence LLM responses. Specifically, a two-stage approach is employed: First, based on the uniqueness of pretraining data in the embedding space, token representations are initially fused for potential copyrighted texts, followed by a lightweight LSTM-based network to analyze dataset contributions. With such a prior, a contrastive-learning-based non-copyright OOD detector is designed. Our framework can dynamically face different situations and bridge the gap between current copyright detection methods. Experiments show that CopyLens improves efficiency and accuracy by 15.2% over our proposed baseline, 58.7% over prompt engineering methods, and 0.21 AUC over OOD detection baselines.
Accelerating Multi-Block Constrained Optimization Through Learning to Optimize
Sep 25, 2024Abstract:Learning to Optimize (L2O) approaches, including algorithm unrolling, plug-and-play methods, and hyperparameter learning, have garnered significant attention and have been successfully applied to the Alternating Direction Method of Multipliers (ADMM) and its variants. However, the natural extension of L2O to multi-block ADMM-type methods remains largely unexplored. Such an extension is critical, as multi-block methods leverage the separable structure of optimization problems, offering substantial reductions in per-iteration complexity. Given that classical multi-block ADMM does not guarantee convergence, the Majorized Proximal Augmented Lagrangian Method (MPALM), which shares a similar form with multi-block ADMM and ensures convergence, is more suitable in this setting. Despite its theoretical advantages, MPALM's performance is highly sensitive to the choice of penalty parameters. To address this limitation, we propose a novel L2O approach that adaptively selects this hyperparameter using supervised learning. We demonstrate the versatility and effectiveness of our method by applying it to the Lasso problem and the optimal transport problem. Our numerical results show that the proposed framework outperforms popular alternatives. Given its applicability to generic linearly constrained composite optimization problems, this work opens the door to a wide range of potential real-world applications.
AdapMoE: Adaptive Sensitivity-based Expert Gating and Management for Efficient MoE Inference
Aug 19, 2024
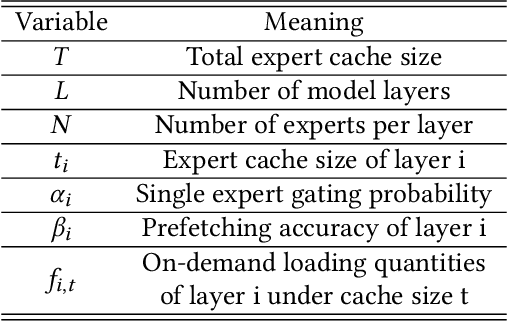
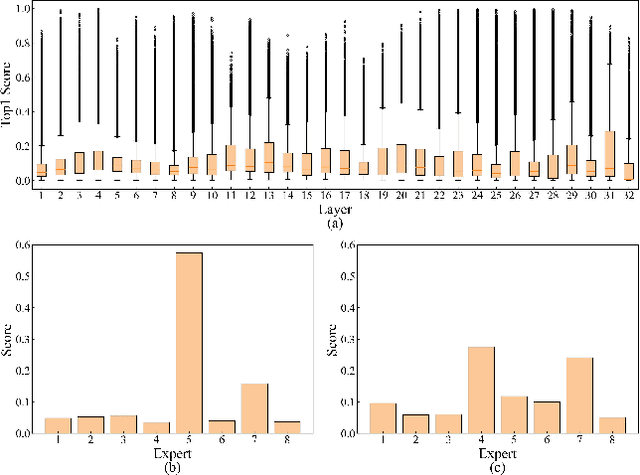
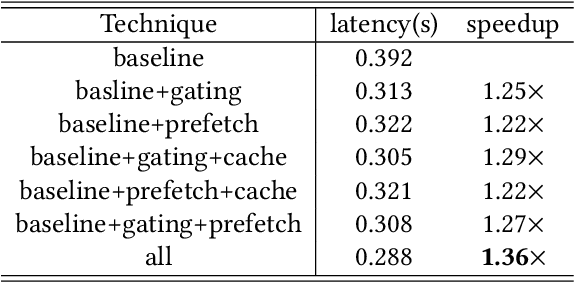
Abstract:Mixture-of-Experts (MoE) models are designed to enhance the efficiency of large language models (LLMs) without proportionally increasing the computational demands. However, their deployment on edge devices still faces significant challenges due to high on-demand loading overheads from managing sparsely activated experts. This paper introduces AdapMoE, an algorithm-system co-design framework for efficient MoE inference. AdapMoE features adaptive expert gating and management to reduce the on-demand loading overheads. We observe the heterogeneity of experts loading across layers and tokens, based on which we propose a sensitivity-based strategy to adjust the number of activated experts dynamically. Meanwhile, we also integrate advanced prefetching and cache management techniques to further reduce the loading latency. Through comprehensive evaluations on various platforms, we demonstrate AdapMoE consistently outperforms existing techniques, reducing the average number of activated experts by 25% and achieving a 1.35x speedup without accuracy degradation. Code is available at: https://github.com/PKU-SEC-Lab/AdapMoE.
The Exploration-Exploitation Dilemma Revisited: An Entropy Perspective
Aug 19, 2024Abstract:The imbalance of exploration and exploitation has long been a significant challenge in reinforcement learning. In policy optimization, excessive reliance on exploration reduces learning efficiency, while over-dependence on exploitation might trap agents in local optima. This paper revisits the exploration-exploitation dilemma from the perspective of entropy by revealing the relationship between entropy and the dynamic adaptive process of exploration and exploitation. Based on this theoretical insight, we establish an end-to-end adaptive framework called AdaZero, which automatically determines whether to explore or to exploit as well as their balance of strength. Experiments show that AdaZero significantly outperforms baseline models across various Atari and MuJoCo environments with only a single setting. Especially in the challenging environment of Montezuma, AdaZero boosts the final returns by up to fifteen times. Moreover, we conduct a series of visualization analyses to reveal the dynamics of our self-adaptive mechanism, demonstrating how entropy reflects and changes with respect to the agent's performance and adaptive process.
TensorTEE: Unifying Heterogeneous TEE Granularity for Efficient Secure Collaborative Tensor Computing
Jul 12, 2024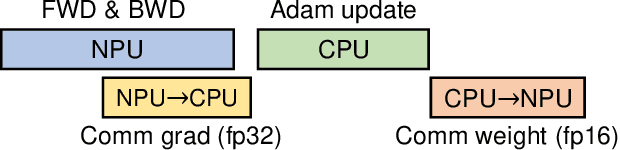
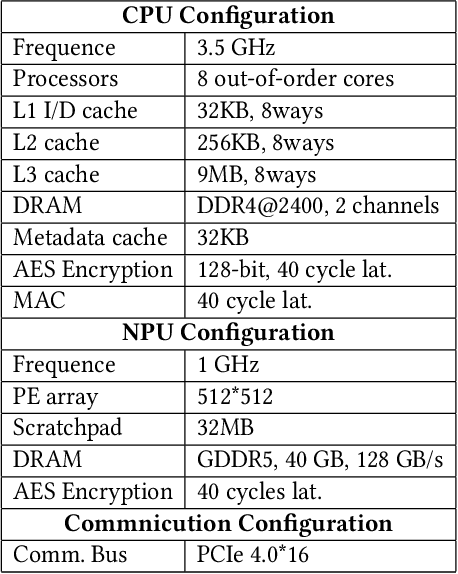
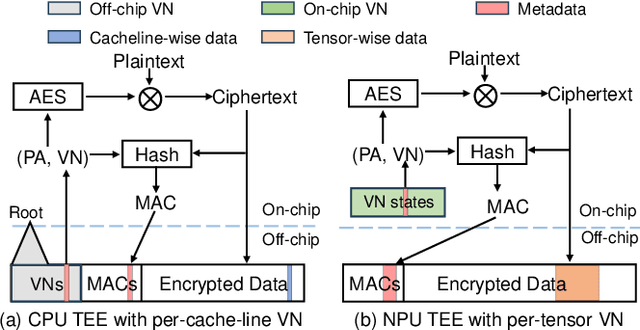
Abstract:Heterogeneous collaborative computing with NPU and CPU has received widespread attention due to its substantial performance benefits. To ensure data confidentiality and integrity during computing, Trusted Execution Environments (TEE) is considered a promising solution because of its comparatively lower overhead. However, existing heterogeneous TEE designs are inefficient for collaborative computing due to fine and different memory granularities between CPU and NPU. 1) The cacheline granularity of CPU TEE intensifies memory pressure due to its extra memory access, and 2) the cacheline granularity MAC of NPU escalates the pressure on the limited memory storage. 3) Data transfer across heterogeneous enclaves relies on the transit of non-secure regions, resulting in cumbersome re-encryption and scheduling. To address these issues, we propose TensorTEE, a unified tensor-granularity heterogeneous TEE for efficient secure collaborative tensor computing. First, we virtually support tensor granularity in CPU TEE to eliminate the off-chip metadata access by detecting and maintaining tensor structures on-chip. Second, we propose tensor-granularity MAC management with predictive execution to avoid computational stalls while eliminating off-chip MAC storage and access. Moreover, based on the unified granularity, we enable direct data transfer without re-encryption and scheduling dilemmas. Our evaluation is built on enhanced Gem5 and a cycle-accurate NPU simulator. The results show that TensorTEE improves the performance of Large Language Model (LLM) training workloads by 4.0x compared to existing work and incurs only 2.1% overhead compared to non-secure training, offering a practical security assurance for LLM training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge