Fairness in Forecasting of Observations of Linear Dynamical Systems
Paper and Code
Sep 16, 2022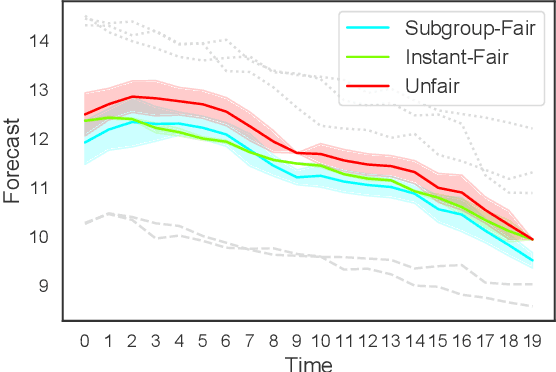
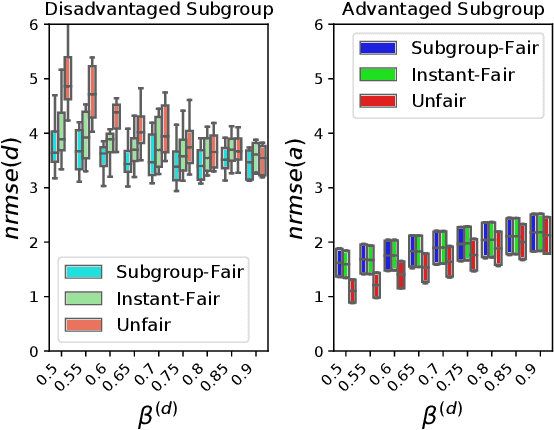

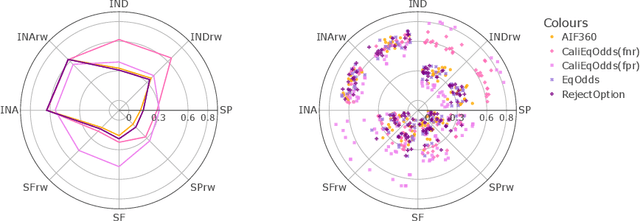
In machine learning, training data often capture the behaviour of multiple subgroups of some underlying human population. When the nature of training data for subgroups are not controlled carefully, under-representation bias arises. To counter this effect we introduce two natural notions of subgroup fairness and instantaneous fairness to address such under-representation bias in time-series forecasting problems. Here we show globally convergent methods for the fairness-constrained learning problems using hierarchies of convexifications of non-commutative polynomial optimisation problems. Our empirical results on a biased data set motivated by insurance applications and the well-known COMPAS data set demonstrate the efficacy of our methods. We also show that by exploiting sparsity in the convexifications, we can reduce the run time of our methods considerably.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge