GLANCE: Global Actions in a Nutshell for Counterfactual Explainability

Counterfactual explanations have emerged as an important tool to understand, debug, and audit complex machine learning models. To offer global counterfactual explainability, state-of-the-art methods construct summaries of local explanations, offering a trade-off among conciseness, counterfactual effectiveness, and counterfactual cost or burden imposed on instances. In this work, we provide a concise formulation of the problem of identifying global counterfactuals and establish principled criteria for comparing solutions, drawing inspiration from Pareto dominance. We introduce innovative algorithms designed to address the challenge of finding global counterfactuals for either the entire input space or specific partitions, employing clustering and decision trees as key components. Additionally, we conduct a comprehensive experimental evaluation, considering various instances of the problem and comparing our proposed algorithms with state-of-the-art methods. The results highlight the consistent capability of our algorithms to generate meaningful and interpretable global counterfactual explanations.

Fairness in Ranking: Robustness through Randomization without the Protected Attribute

There has been great interest in fairness in machine learning, especially in relation to classification problems. In ranking-related problems, such as in online advertising, recommender systems, and HR automation, much work on fairness remains to be done. Two complications arise: first, the protected attribute may not be available in many applications. Second, there are multiple measures of fairness of rankings, and optimization-based methods utilizing a single measure of fairness of rankings may produce rankings that are unfair with respect to other measures. In this work, we propose a randomized method for post-processing rankings, which do not require the availability of the protected attribute. In an extensive numerical study, we show the robustness of our methods with respect to P-Fairness and effectiveness with respect to Normalized Discounted Cumulative Gain (NDCG) from the baseline ranking, improving on previously proposed methods.

Fairness Aware Counterfactuals for Subgroups

In this work, we present Fairness Aware Counterfactuals for Subgroups (FACTS), a framework for auditing subgroup fairness through counterfactual explanations. We start with revisiting (and generalizing) existing notions and introducing new, more refined notions of subgroup fairness. We aim to (a) formulate different aspects of the difficulty of individuals in certain subgroups to achieve recourse, i.e. receive the desired outcome, either at the micro level, considering members of the subgroup individually, or at the macro level, considering the subgroup as a whole, and (b) introduce notions of subgroup fairness that are robust, if not totally oblivious, to the cost of achieving recourse. We accompany these notions with an efficient, model-agnostic, highly parameterizable, and explainable framework for evaluating subgroup fairness. We demonstrate the advantages, the wide applicability, and the efficiency of our approach through a thorough experimental evaluation of different benchmark datasets.

Label Ranking through Nonparametric Regression

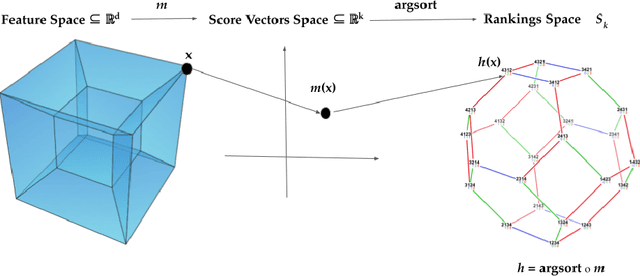
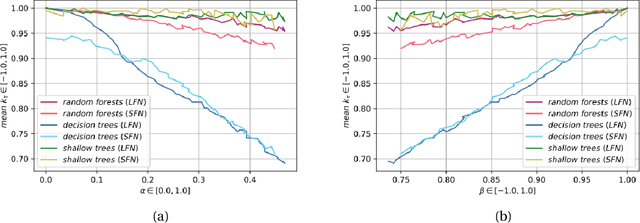
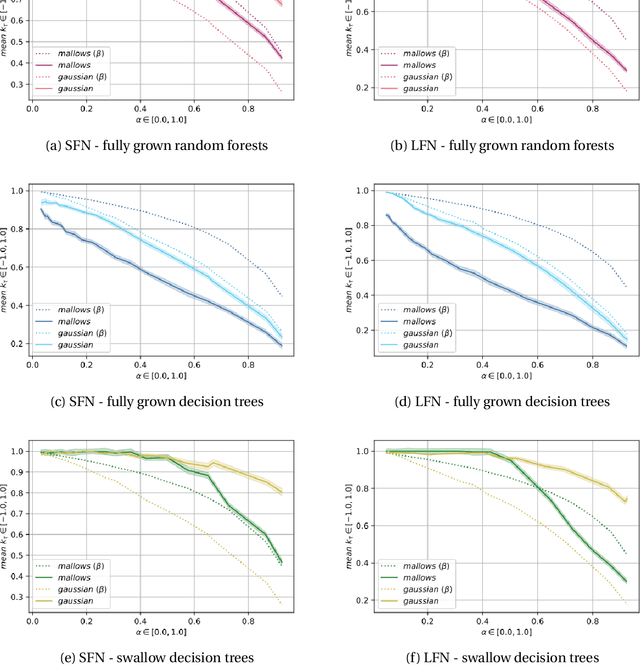
Label Ranking (LR) corresponds to the problem of learning a hypothesis that maps features to rankings over a finite set of labels. We adopt a nonparametric regression approach to LR and obtain theoretical performance guarantees for this fundamental practical problem. We introduce a generative model for Label Ranking, in noiseless and noisy nonparametric regression settings, and provide sample complexity bounds for learning algorithms in both cases. In the noiseless setting, we study the LR problem with full rankings and provide computationally efficient algorithms using decision trees and random forests in the high-dimensional regime. In the noisy setting, we consider the more general cases of LR with incomplete and partial rankings from a statistical viewpoint and obtain sample complexity bounds using the One-Versus-One approach of multiclass classification. Finally, we complement our theoretical contributions with experiments, aiming to understand how the input regression noise affects the observed output.