Deep Copula-Based Survival Analysis for Dependent Censoring with Identifiability Guarantees

Censoring is the central problem in survival analysis where either the time-to-event (for instance, death), or the time-tocensoring (such as loss of follow-up) is observed for each sample. The majority of existing machine learning-based survival analysis methods assume that survival is conditionally independent of censoring given a set of covariates; an assumption that cannot be verified since only marginal distributions is available from the data. The existence of dependent censoring, along with the inherent bias in current estimators has been demonstrated in a variety of applications, accentuating the need for a more nuanced approach. However, existing methods that adjust for dependent censoring require practitioners to specify the ground truth copula. This requirement poses a significant challenge for practical applications, as model misspecification can lead to substantial bias. In this work, we propose a flexible deep learning-based survival analysis method that simultaneously accommodate for dependent censoring and eliminates the requirement for specifying the ground truth copula. We theoretically prove the identifiability of our model under a broad family of copulas and survival distributions. Experiments results from a wide range of datasets demonstrate that our approach successfully discerns the underlying dependency structure and significantly reduces survival estimation bias when compared to existing methods.

Multi-defender Security Games with Schedules

Stackelberg Security Games are often used to model strategic interactions in high-stakes security settings. The majority of existing models focus on single-defender settings where a single entity assumes command of all security assets. However, many realistic scenarios feature multiple heterogeneous defenders with their own interests and priorities embedded in a more complex system. Furthermore, defenders rarely choose targets to protect. Instead, they have a multitude of defensive resources or schedules at its disposal, each with different protective capabilities. In this paper, we study security games featuring multiple defenders and schedules simultaneously. We show that unlike prior work on multi-defender security games, the introduction of schedules can cause non-existence of equilibrium even under rather restricted environments. We prove that under the mild restriction that any subset of a schedule is also a schedule, non-existence of equilibrium is not only avoided, but can be computed in polynomial time in games with two defenders. Under additional assumptions, our algorithm can be extended to games with more than two defenders and its computation scaled up in special classes of games with compactly represented schedules such as those used in patrolling applications. Experimental results suggest that our methods scale gracefully with game size, making our algorithms amongst the few that can tackle multiple heterogeneous defenders.

Multimodal Learning Without Labeled Multimodal Data: Guarantees and Applications

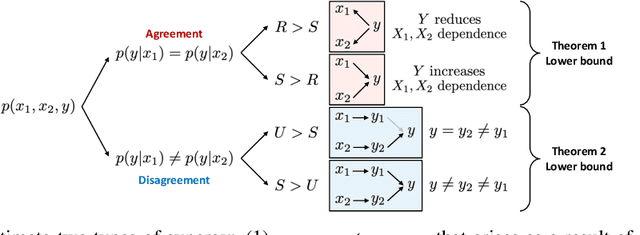
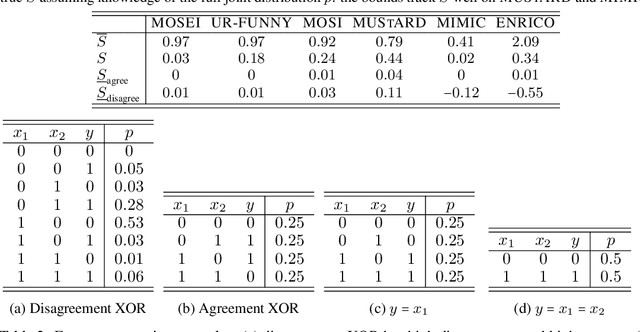
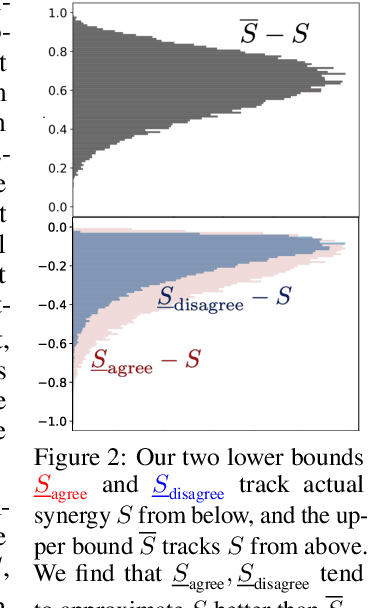
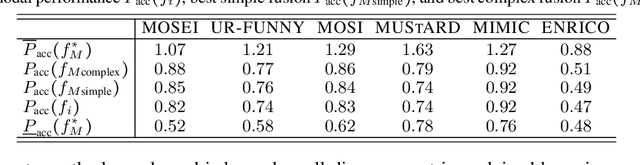
In many machine learning systems that jointly learn from multiple modalities, a core research question is to understand the nature of multimodal interactions: the emergence of new task-relevant information during learning from both modalities that was not present in either alone. We study this challenge of interaction quantification in a semi-supervised setting with only labeled unimodal data and naturally co-occurring multimodal data (e.g., unlabeled images and captions, video and corresponding audio) but when labeling them is time-consuming. Using a precise information-theoretic definition of interactions, our key contributions are the derivations of lower and upper bounds to quantify the amount of multimodal interactions in this semi-supervised setting. We propose two lower bounds based on the amount of shared information between modalities and the disagreement between separately trained unimodal classifiers, and derive an upper bound through connections to approximate algorithms for min-entropy couplings. We validate these estimated bounds and show how they accurately track true interactions. Finally, two semi-supervised multimodal applications are explored based on these theoretical results: (1) analyzing the relationship between multimodal performance and estimated interactions, and (2) self-supervised learning that embraces disagreement between modalities beyond agreement as is typically done.

Quantifying & Modeling Feature Interactions: An Information Decomposition Framework

The recent explosion of interest in multimodal applications has resulted in a wide selection of datasets and methods for representing and integrating information from different signals. Despite these empirical advances, there remain fundamental research questions: how can we quantify the nature of interactions that exist among input features? Subsequently, how can we capture these interactions using suitable data-driven methods? To answer this question, we propose an information-theoretic approach to quantify the degree of redundancy, uniqueness, and synergy across input features, which we term the PID statistics of a multimodal distribution. Using 2 newly proposed estimators that scale to high-dimensional distributions, we demonstrate their usefulness in quantifying the interactions within multimodal datasets, the nature of interactions captured by multimodal models, and principled approaches for model selection. We conduct extensive experiments on both synthetic datasets where the PID statistics are known and on large-scale multimodal benchmarks where PID estimation was previously impossible. Finally, to demonstrate the real-world applicability of our approach, we present three case studies in pathology, mood prediction, and robotic perception where our framework accurately recommends strong multimodal models for each application.

Abstracting Imperfect Information Away from Two-Player Zero-Sum Games

In their seminal work, Nayyar et al. (2013) showed that imperfect information can be abstracted away from common-payoff games by having players publicly announce their policies as they play. This insight underpins sound solvers and decision-time planning algorithms for common-payoff games. Unfortunately, a naive application of the same insight to two-player zero-sum games fails because Nash equilibria of the game with public policy announcements may not correspond to Nash equilibria of the original game. As a consequence, existing sound decision-time planning algorithms require complicated additional mechanisms that have unappealing properties. The main contribution of this work is showing that certain regularized equilibria do not possess the aforementioned non-correspondence problem -- thus, computing them can be treated as perfect information problems. Because these regularized equilibria can be made arbitrarily close to Nash equilibria, our result opens the door to a new perspective on solving two-player zero-sum games and, in particular, yields a simplified framework for decision-time planning in two-player zero-sum games, void of the unappealing properties that plague existing decision-time planning approaches.

Function Approximation for Solving Stackelberg Equilibrium in Large Perfect Information Games

Function approximation (FA) has been a critical component in solving large zero-sum games. Yet, little attention has been given towards FA in solving \textit{general-sum} extensive-form games, despite them being widely regarded as being computationally more challenging than their fully competitive or cooperative counterparts. A key challenge is that for many equilibria in general-sum games, no simple analogue to the state value function used in Markov Decision Processes and zero-sum games exists. In this paper, we propose learning the \textit{Enforceable Payoff Frontier} (EPF) -- a generalization of the state value function for general-sum games. We approximate the optimal \textit{Stackelberg extensive-form correlated equilibrium} by representing EPFs with neural networks and training them by using appropriate backup operations and loss functions. This is the first method that applies FA to the Stackelberg setting, allowing us to scale to much larger games while still enjoying performance guarantees based on FA error. Additionally, our proposed method guarantees incentive compatibility and is easy to evaluate without having to depend on self-play or approximate best-response oracles.

Safe Subgame Resolving for Extensive Form Correlated Equilibrium

Correlated Equilibrium is a solution concept that is more general than Nash Equilibrium (NE) and can lead to outcomes with better social welfare. However, its natural extension to the sequential setting, the \textit{Extensive Form Correlated Equilibrium} (EFCE), requires a quadratic amount of space to solve, even in restricted settings without randomness in nature. To alleviate these concerns, we apply \textit{subgame resolving}, a technique extremely successful in finding NE in zero-sum games to solving general-sum EFCEs. Subgame resolving refines a correlation plan in an \textit{online} manner: instead of solving for the full game upfront, it only solves for strategies in subgames that are reached in actual play, resulting in significant computational gains. In this paper, we (i) lay out the foundations to quantify the quality of a refined strategy, in terms of the \textit{social welfare} and \textit{exploitability} of correlation plans, (ii) show that EFCEs possess a sufficient amount of independence between subgames to perform resolving efficiently, and (iii) provide two algorithms for resolving, one using linear programming and the other based on regret minimization. Both methods guarantee \textit{safety}, i.e., they will never be counterproductive. Our methods are the first time an online method has been applied to the correlated, general-sum setting.

Safe Search for Stackelberg Equilibria in Extensive-Form Games

Stackelberg equilibrium is a solution concept in two-player games where the leader has commitment rights over the follower. In recent years, it has become a cornerstone of many security applications, including airport patrolling and wildlife poaching prevention. Even though many of these settings are sequential in nature, existing techniques pre-compute the entire solution ahead of time. In this paper, we present a theoretically sound and empirically effective way to apply search, which leverages extra online computation to improve a solution, to the computation of Stackelberg equilibria in general-sum games. Instead of the leader attempting to solve the full game upfront, an approximate "blueprint" solution is first computed offline and is then improved online for the particular subgames encountered in actual play. We prove that our search technique is guaranteed to perform no worse than the pre-computed blueprint strategy, and empirically demonstrate that it enables approximately solving significantly larger games compared to purely offline methods. We also show that our search operation may be cast as a smaller Stackelberg problem, making our method complementary to existing algorithms based on strategy generation.

Deep Archimedean Copulas

A central problem in machine learning and statistics is to model joint densities of random variables from data. Copulas are joint cumulative distribution functions with uniform marginal distributions and are used to capture interdependencies in isolation from marginals. Copulas are widely used within statistics, but have not gained traction in the context of modern deep learning. In this paper, we introduce ACNet, a novel differentiable neural network architecture that enforces structural properties and enables one to learn an important class of copulas--Archimedean Copulas. Unlike Generative Adversarial Networks, Variational Autoencoders, or Normalizing Flow methods, which learn either densities or the generative process directly, ACNet learns a generator of the copula, which implicitly defines the cumulative distribution function of a joint distribution. We give a probabilistic interpretation of the network parameters of ACNet and use this to derive a simple but efficient sampling algorithm for the learned copula. Our experiments show that ACNet is able to both approximate common Archimedean Copulas and generate new copulas which may provide better fits to data.