Online Learning under Adversarial Nonlinear Constraints
Paper and Code
Jun 06, 2023
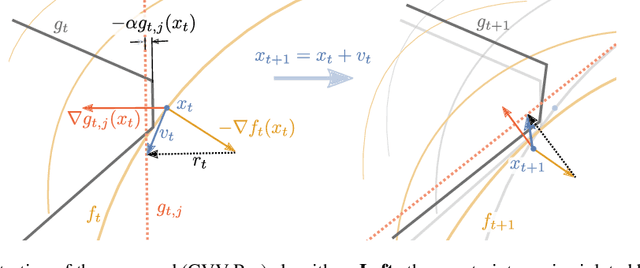

In many applications, learning systems are required to process continuous non-stationary data streams. We study this problem in an online learning framework and propose an algorithm that can deal with adversarial time-varying and nonlinear constraints. As we show in our work, the algorithm called Constraint Violation Velocity Projection (CVV-Pro) achieves $\sqrt{T}$ regret and converges to the feasible set at a rate of $1/\sqrt{T}$, despite the fact that the feasible set is slowly time-varying and a priori unknown to the learner. CVV-Pro only relies on local sparse linear approximations of the feasible set and therefore avoids optimizing over the entire set at each iteration, which is in sharp contrast to projected gradients or Frank-Wolfe methods. We also empirically evaluate our algorithm on two-player games, where the players are subjected to a shared constraint.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge