Reinforcement Learning for Finite Space Mean-Field Type Games
Paper and Code
Sep 25, 2024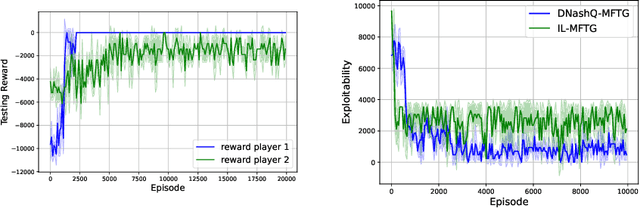

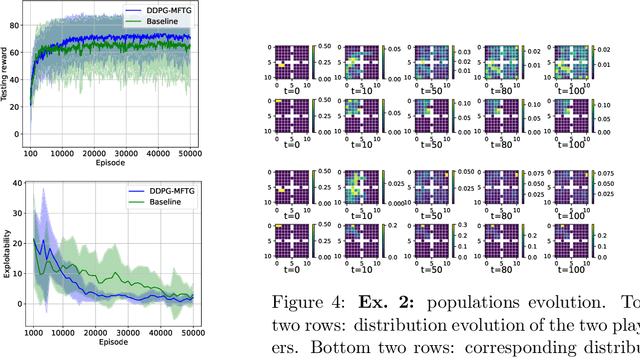
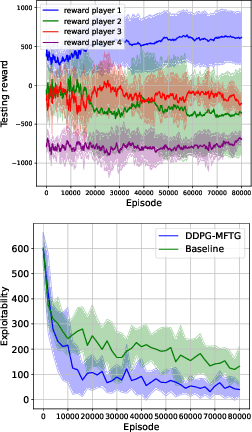
Mean field type games (MFTGs) describe Nash equilibria between large coalitions: each coalition consists of a continuum of cooperative agents who maximize the average reward of their coalition while interacting non-cooperatively with a finite number of other coalitions. Although the theory has been extensively developed, we are still lacking efficient and scalable computational methods. Here, we develop reinforcement learning methods for such games in a finite space setting with general dynamics and reward functions. We start by proving that MFTG solution yields approximate Nash equilibria in finite-size coalition games. We then propose two algorithms. The first is based on quantization of the mean-field spaces and Nash Q-learning. We provide convergence and stability analysis. We then propose an deep reinforcement learning algorithm, which can scale to larger spaces. Numerical examples on 5 environments show the scalability and the efficiency of the proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge