Graph-MLLM: Harnessing Multimodal Large Language Models for Multimodal Graph Learning

Multimodal Large Language Models (MLLMs) have demonstrated remarkable capabilities in representing and understanding diverse modalities. However, they typically focus on modality alignment in a pairwise manner while overlooking structural relationships across data points. Integrating multimodality with structured graph information (i.e., multimodal graphs, MMGs) is essential for real-world applications such as social networks, healthcare, and recommendation systems. Existing MMG learning methods fall into three paradigms based on how they leverage MLLMs: Encoder, Aligner, and Predictor. MLLM-as-Encoder focuses on enhancing graph neural networks (GNNs) via multimodal feature fusion; MLLM-as-Aligner aligns multimodal attributes in language or hidden space to enable LLM-based graph reasoning; MLLM-as-Predictor treats MLLMs as standalone reasoners with in-context learning or fine-tuning. Despite their advances, the MMG field lacks a unified benchmark to fairly evaluate across these approaches, making it unclear what progress has been made. To bridge this gap, we present Graph-MLLM, a comprehensive benchmark for multimodal graph learning by systematically evaluating these three paradigms across six datasets with different domains. Through extensive experiments, we observe that jointly considering the visual and textual attributes of the nodes benefits graph learning, even when using pre-trained text-to-image alignment models (e.g., CLIP) as encoders. We also find that converting visual attributes into textual descriptions further improves performance compared to directly using visual inputs. Moreover, we observe that fine-tuning MLLMs on specific MMGs can achieve state-of-the-art results in most scenarios, even without explicit graph structure information. We hope that our open-sourced library will facilitate rapid, equitable evaluation and inspire further innovative research in this field.

GRAPHGPT-O: Synergistic Multimodal Comprehension and Generation on Graphs

The rapid development of Multimodal Large Language Models (MLLMs) has enabled the integration of multiple modalities, including texts and images, within the large language model (LLM) framework. However, texts and images are usually interconnected, forming a multimodal attributed graph (MMAG). It is underexplored how MLLMs can incorporate the relational information (\textit{i.e.}, graph structure) and semantic information (\textit{i.e.,} texts and images) on such graphs for multimodal comprehension and generation. In this paper, we propose GraphGPT-o, which supports omni-multimodal understanding and creation on MMAGs. We first comprehensively study linearization variants to transform semantic and structural information as input for MLLMs. Then, we propose a hierarchical aligner that enables deep graph encoding, bridging the gap between MMAGs and MLLMs. Finally, we explore the inference choices, adapting MLLM to interleaved text and image generation in graph scenarios. Extensive experiments on three datasets from different domains demonstrate the effectiveness of our proposed method. Datasets and codes will be open-sourced upon acceptance.

Reinforcement Learning for Finite Space Mean-Field Type Games

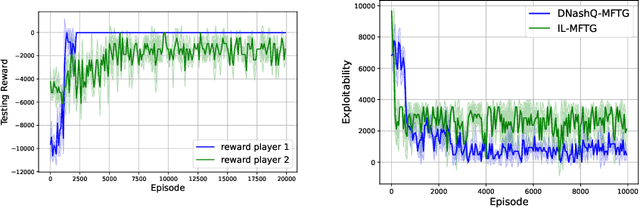
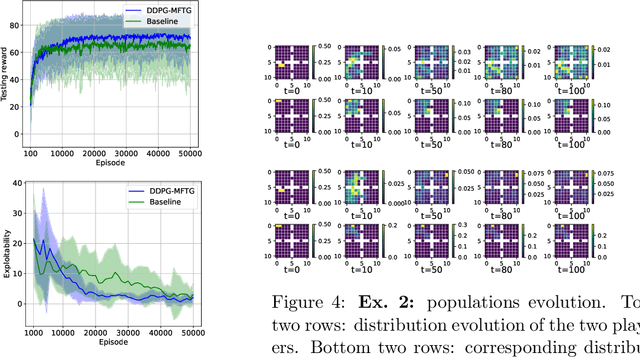
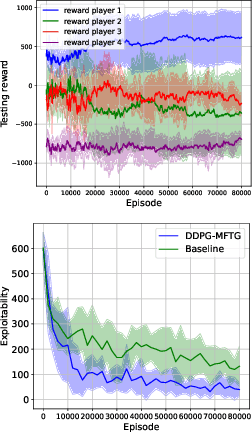
Mean field type games (MFTGs) describe Nash equilibria between large coalitions: each coalition consists of a continuum of cooperative agents who maximize the average reward of their coalition while interacting non-cooperatively with a finite number of other coalitions. Although the theory has been extensively developed, we are still lacking efficient and scalable computational methods. Here, we develop reinforcement learning methods for such games in a finite space setting with general dynamics and reward functions. We start by proving that MFTG solution yields approximate Nash equilibria in finite-size coalition games. We then propose two algorithms. The first is based on quantization of the mean-field spaces and Nash Q-learning. We provide convergence and stability analysis. We then propose an deep reinforcement learning algorithm, which can scale to larger spaces. Numerical examples on 5 environments show the scalability and the efficiency of the proposed method.

CM-DQN: A Value-Based Deep Reinforcement Learning Model to Simulate Confirmation Bias

In human decision-making tasks, individuals learn through trials and prediction errors. When individuals learn the task, some are more influenced by good outcomes, while others weigh bad outcomes more heavily. Such confirmation bias can lead to different learning effects. In this study, we propose a new algorithm in Deep Reinforcement Learning, CM-DQN, which applies the idea of different update strategies for positive or negative prediction errors, to simulate the human decision-making process when the task's states are continuous while the actions are discrete. We test in Lunar Lander environment with confirmatory, disconfirmatory bias and non-biased to observe the learning effects. Moreover, we apply the confirmation model in a multi-armed bandit problem (environment in discrete states and discrete actions), which utilizes the same idea as our proposed algorithm, as a contrast experiment to algorithmically simulate the impact of different confirmation bias in decision-making process. In both experiments, confirmatory bias indicates a better learning effect. Our code can be found here https://github.com/Patrickhshs/CM-DQN.