Unsupervised Discovery of Clinical Disease Signatures Using Probabilistic Independence

Insufficiently precise diagnosis of clinical disease is likely responsible for many treatment failures, even for common conditions and treatments. With a large enough dataset, it may be possible to use unsupervised machine learning to define clinical disease patterns more precisely. We present an approach to learning these patterns by using probabilistic independence to disentangle the imprint on the medical record of causal latent sources of disease. We inferred a broad set of 2000 clinical signatures of latent sources from 9195 variables in 269,099 Electronic Health Records. The learned signatures produced better discrimination than the original variables in a lung cancer prediction task unknown to the inference algorithm, predicting 3-year malignancy in patients with no history of cancer before a solitary lung nodule was discovered. More importantly, the signatures' greater explanatory power identified pre-nodule signatures of apparently undiagnosed cancer in many of those patients.

Why Do Clinical Probabilistic Models Fail To Transport Between Sites?

The rising popularity of artificial intelligence in healthcare is highlighting the problem that a computational model achieving super-human clinical performance at its training sites may perform substantially worse at new sites. In this perspective, we present common sources for this failure to transport, which we divide into sources under the control of the experimenter and sources inherent to the clinical data-generating process. Of the inherent sources we look a little deeper into site-specific clinical practices that can affect the data distribution, and propose a potential solution intended to isolate the imprint of those practices on the data from the patterns of disease cause and effect that are the usual target of clinical models.

Counterfactual Formulation of Patient-Specific Root Causes of Disease

Root causes of disease intuitively correspond to root vertices that increase the likelihood of a diagnosis. This description of a root cause nevertheless lacks the rigorous mathematical formulation needed for the development of computer algorithms designed to automatically detect root causes from data. Prior work defined patient-specific root causes of disease using an interventionalist account that only climbs to the second rung of Pearl's Ladder of Causation. In this theoretical piece, we climb to the third rung by proposing a counterfactual definition matching clinical intuition based on fixed factual data alone. We then show how to assign a root causal contribution score to each variable using Shapley values from explainable artificial intelligence. The proposed counterfactual formulation of patient-specific root causes of disease accounts for noisy labels, adapts to disease prevalence and admits fast computation without the need for counterfactual simulation.

Sample-Specific Root Causal Inference with Latent Variables

Root causal analysis seeks to identify the set of initial perturbations that induce an unwanted outcome. In prior work, we defined sample-specific root causes of disease using exogenous error terms that predict a diagnosis in a structural equation model. We rigorously quantified predictivity using Shapley values. However, the associated algorithms for inferring root causes assume no latent confounding. We relax this assumption by permitting confounding among the predictors. We then introduce a corresponding procedure called Extract Errors with Latents (EEL) for recovering the error terms up to contamination by vertices on certain paths under the linear non-Gaussian acyclic model. EEL also identifies the smallest sets of dependent errors for fast computation of the Shapley values. The algorithm bypasses the hard problem of estimating the underlying causal graph in both cases. Experiments highlight the superior accuracy and robustness of EEL relative to its predecessors.

Identifying Patient-Specific Root Causes with the Heteroscedastic Noise Model

Complex diseases are caused by a multitude of factors that may differ between patients even within the same diagnostic category. A few underlying root causes may nevertheless initiate the development of disease within each patient. We therefore focus on identifying patient-specific root causes of disease, which we equate to the sample-specific predictivity of the exogenous error terms in a structural equation model. We generalize from the linear setting to the heteroscedastic noise model where $Y = m(X) + \varepsilon\sigma(X)$ with non-linear functions $m(X)$ and $\sigma(X)$ representing the conditional mean and mean absolute deviation, respectively. This model preserves identifiability but introduces non-trivial challenges that require a customized algorithm called Generalized Root Causal Inference (GRCI) to extract the error terms correctly. GRCI recovers patient-specific root causes more accurately than existing alternatives.

Identifying Patient-Specific Root Causes of Disease

Complex diseases are caused by a multitude of factors that may differ between patients. As a result, hypothesis tests comparing all patients to all healthy controls can detect many significant variables with inconsequential effect sizes. A few highly predictive root causes may nevertheless generate disease within each patient. In this paper, we define patient-specific root causes as variables subject to exogenous "shocks" which go on to perturb an otherwise healthy system and induce disease. In other words, the variables are associated with the exogenous errors of a structural equation model (SEM), and these errors predict a downstream diagnostic label. We quantify predictivity using sample-specific Shapley values. This derivation allows us to develop a fast algorithm called Root Causal Inference for identifying patient-specific root causes by extracting the error terms of a linear SEM and then computing the Shapley value associated with each error. Experiments highlight considerable improvements in accuracy because the method uncovers root causes that may have large effect sizes at the individual level but clinically insignificant effect sizes at the group level. An R implementation is available at github.com/ericstrobl/RCI.

Generalizing Clinical Trials with Convex Hulls

Randomized clinical trials eliminate confounding but impose strict exclusion criteria that limit recruitment to a subset of the population. Observational datasets are more inclusive but suffer from confounding -- often providing overly optimistic estimates of treatment effect in practice. We therefore assume that the true treatment effect lies somewhere in between no treatment effect and the observational estimate, or in their convex hull. This assumption allows us to extrapolate results from exclusive trials to the broader population by analyzing observational and trial data simultaneously using an algorithm called Optimal Convex Hulls (OCH). OCH represents the treatment effect either in terms of convex hulls of conditional expectations or convex hulls (also known as mixtures) of conditional densities. The algorithm first learns the component expectations or densities using the observational data and then learns the linear mixing coefficients using trial data in order to approximate the true treatment effect; theory importantly explains why this linear combination should hold. OCH estimates the treatment effect in terms both expectations and densities with state of the art accuracy.

Synthesized Difference in Differences

Randomized clinical trials (RCTs) eliminate confounding but impose strict exclusion criteria that prevent sampling of the entire clinical population. Observational datasets are more inclusive but suffer from confounding. Difference in Differences (DD) eliminates confounding from observational data by comparing outcomes before and after treatment administration. However, the algorithm requires a parallel slopes assumption that may not apply in practice when confounding shifts across time. In this paper, we propose Synthesized Difference in Differences (SDD) that infers the correct (possibly non-parallel) slopes by linearly adjusting a conditional version of DD using additional RCT data. The algorithm achieves state of the art performance across multiple synthetic and real datasets even when the RCT excludes the majority of patients.

Automated Hyperparameter Selection for the PC Algorithm

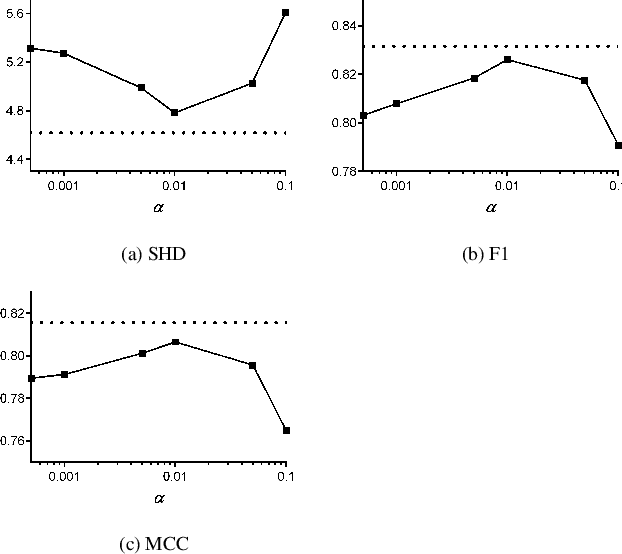
The PC algorithm infers causal relations using conditional independence tests that require a pre-specified Type I $\alpha$ level. PC is however unsupervised, so we cannot tune $\alpha$ using traditional cross-validation. We therefore propose AutoPC, a fast procedure that optimizes $\alpha$ directly for a user chosen metric. We in particular force PC to double check its output by executing a second run on the recovered graph. We choose the final output as the one which maximizes stability between the two runs. AutoPC consistently outperforms the state of the art across multiple metrics.

Dirac Delta Regression: Conditional Density Estimation with Clinical Trials

Personalized medicine seeks to identify the causal effect of treatment for a particular patient as opposed to a clinical population at large. Most investigators estimate such personalized treatment effects by regressing the outcome of a randomized clinical trial (RCT) on patient covariates. The realized value of the outcome may however lie far from the conditional expectation. We therefore introduce a method called Dirac Delta Regression (DDR) that estimates the entire conditional density from RCT data in order to visualize the probabilities across all possible treatment outcomes. DDR transforms the outcome into a set of asymptotically Dirac delta distributions and then estimates the density using non-linear regression. The algorithm can identify significant patient-specific treatment effects even when no population level effect exists. Moreover, DDR outperforms state-of-the-art algorithms in conditional density estimation on average regardless of the need for causal inference.