Directed Cyclic Graphical Representations of Feedback Models
Paper and Code
Feb 20, 2013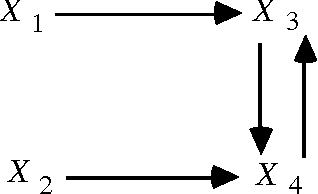



The use of directed acyclic graphs (DAGs) to represent conditional independence relations among random variables has proved fruitful in a variety of ways. Recursive structural equation models are one kind of DAG model. However, non-recursive structural equation models of the kinds used to model economic processes are naturally represented by directed cyclic graphs with independent errors, a characterization of conditional independence errors, a characterization of conditional independence constraints is obtained, and it is shown that the result generalizes in a natural way to systems in which the error variables or noises are statistically dependent. For non-linear systems with independent errors a sufficient condition for conditional independence of variables in associated distributions is obtained.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge