Calculation of Entailed Rank Constraints in Partially Non-Linear and Cyclic Models
Paper and Code
Sep 17, 2013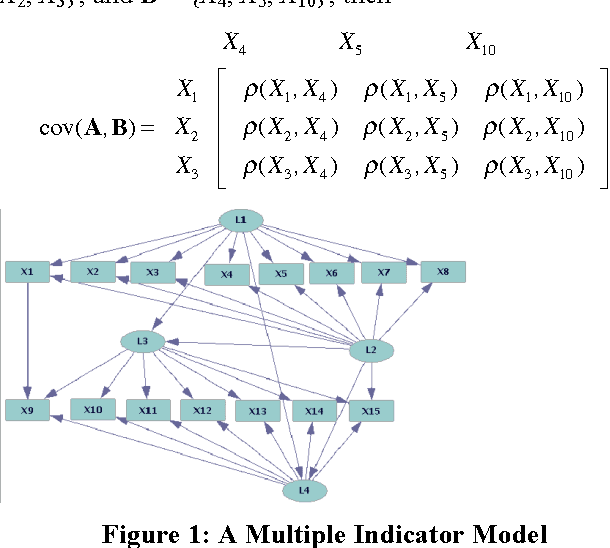
The Trek Separation Theorem (Sullivant et al. 2010) states necessary and sufficient conditions for a linear directed acyclic graphical model to entail for all possible values of its linear coefficients that the rank of various sub-matrices of the covariance matrix is less than or equal to n, for any given n. In this paper, I extend the Trek Separation Theorem in two ways: I prove that the same necessary and sufficient conditions apply even when the generating model is partially non-linear and contains some cycles. This justifies application of constraint-based causal search algorithms such as the BuildPureClusters algorithm (Silva et al. 2006) for discovering the causal structure of latent variable models to data generated by a wider class of causal models that may contain non-linear and cyclic relations among the latent variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge