Estimating and Controlling the False Discovery Rate for the PC Algorithm Using Edge-Specific P-Values
Paper and Code
May 10, 2017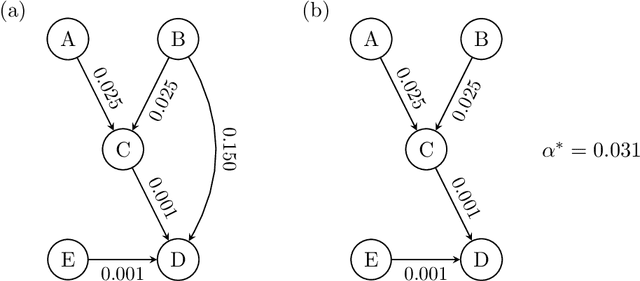
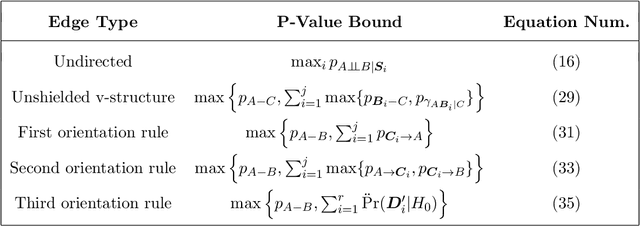
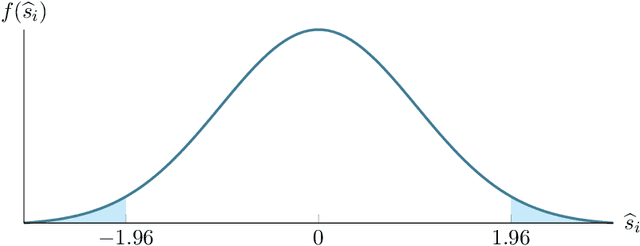

The PC algorithm allows investigators to estimate a complete partially directed acyclic graph (CPDAG) from a finite dataset, but few groups have investigated strategies for estimating and controlling the false discovery rate (FDR) of the edges in the CPDAG. In this paper, we introduce PC with p-values (PC-p), a fast algorithm which robustly computes edge-specific p-values and then estimates and controls the FDR across the edges. PC-p specifically uses the p-values returned by many conditional independence tests to upper bound the p-values of more complex edge-specific hypothesis tests. The algorithm then estimates and controls the FDR using the bounded p-values and the Benjamini-Yekutieli FDR procedure. Modifications to the original PC algorithm also help PC-p accurately compute the upper bounds despite non-zero Type II error rates. Experiments show that PC-p yields more accurate FDR estimation and control across the edges in a variety of CPDAGs compared to alternative methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge