Learning Measurement Models for Unobserved Variables
Paper and Code
Oct 19, 2012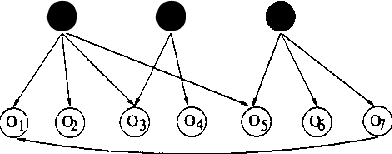
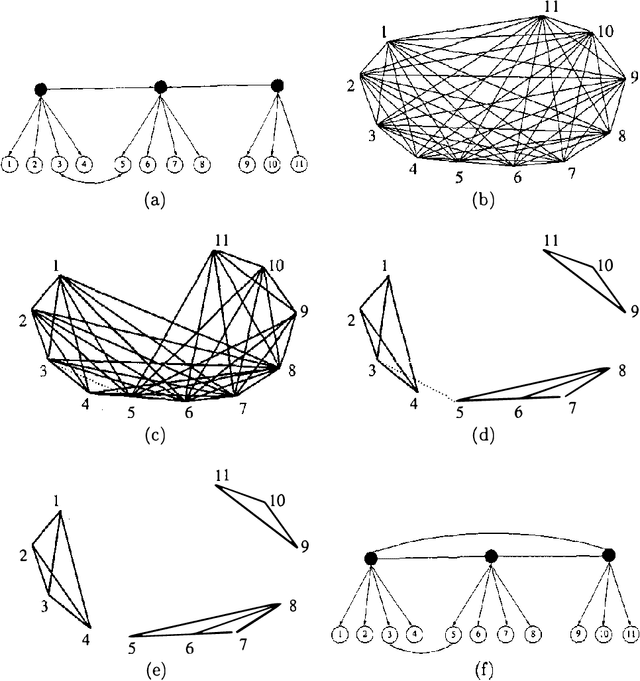
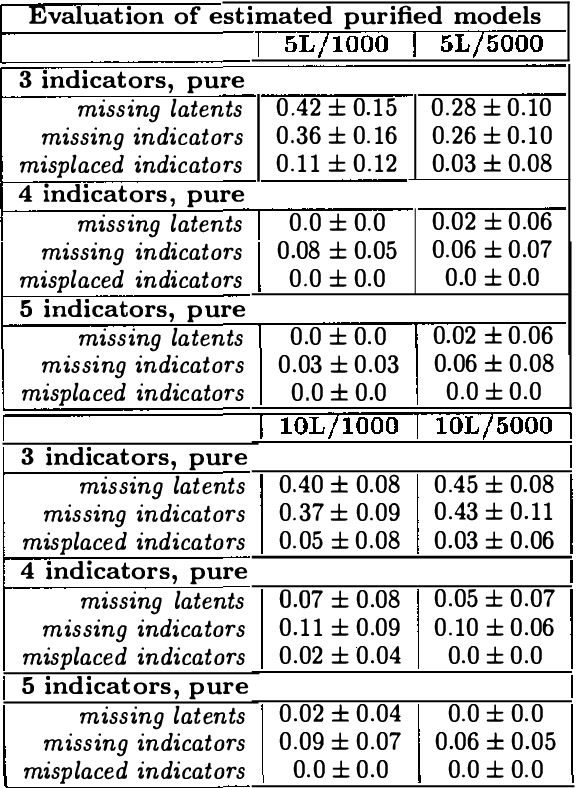

Observed associations in a database may be due in whole or part to variations in unrecorded (latent) variables. Identifying such variables and their causal relationships with one another is a principal goal in many scientific and practical domains. Previous work shows that, given a partition of observed variables such that members of a class share only a single latent common cause, standard search algorithms for causal Bayes nets can infer structural relations between latent variables. We introduce an algorithm for discovering such partitions when they exist. Uniquely among available procedures, the algorithm is (asymptotically) correct under standard assumptions in causal Bayes net search algorithms, requires no prior knowledge of the number of latent variables, and does not depend on the mathematical form of the relationships among the latent variables. We evaluate the algorithm on a variety of simulated data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge