Causal Discovery with Multi-Domain LiNGAM for Latent Factors

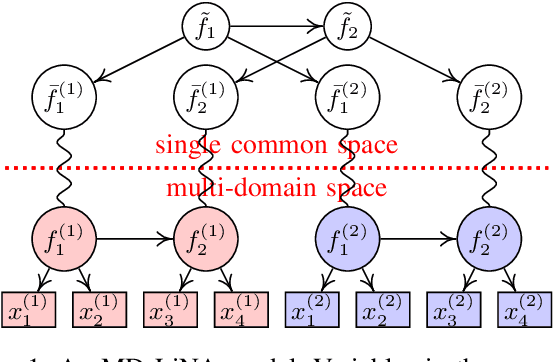
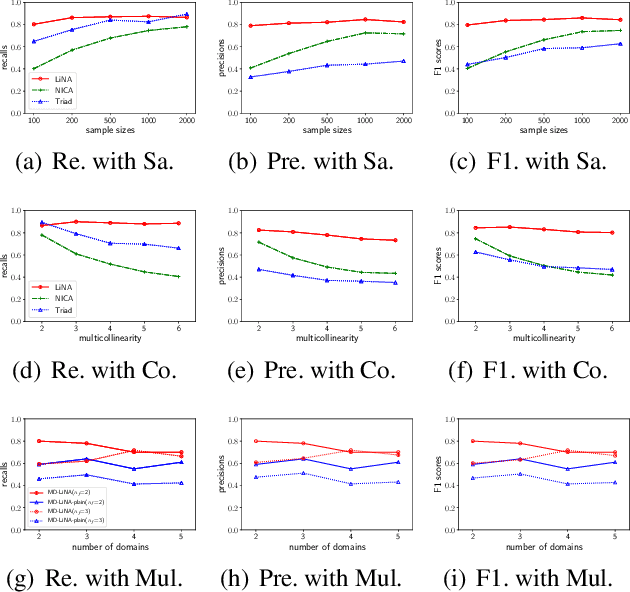
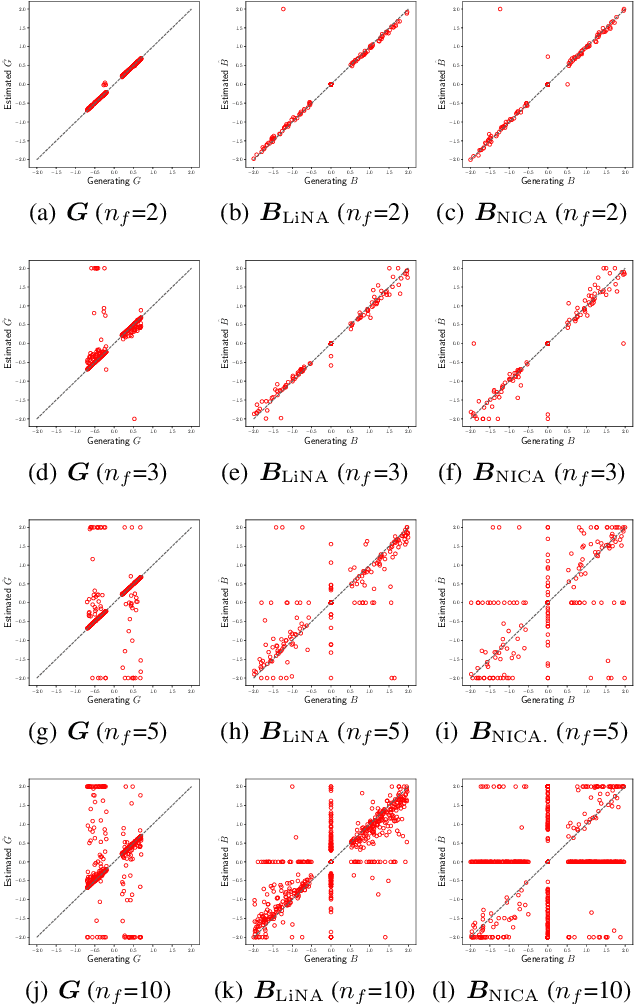
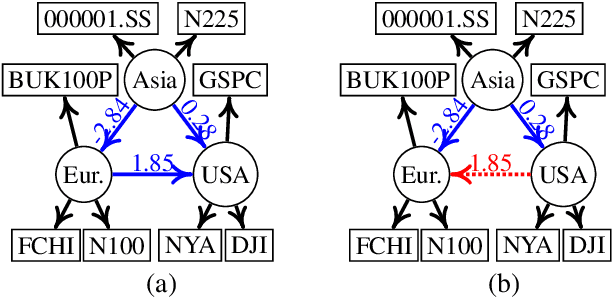
Discovering causal structures among latent factors from observed data is a particularly challenging problem, in which many empirical researchers are interested. Despite its success in certain degrees, existing methods focus on the single-domain observed data only, while in many scenarios data may be originated from distinct domains, e.g. in neuroinformatics. In this paper, we propose Multi-Domain Linear Non-Gaussian Acyclic Models for LAtent Factors (abbreviated as MD-LiNA model) to identify the underlying causal structure between latent factors (of interest), tackling not only single-domain observed data but multiple-domain ones, and provide its identification results. In particular, we first locate the latent factors and estimate the factor loadings matrix for each domain separately. Then to estimate the structure among latent factors (of interest), we derive a score function based on the characterization of independence relations between external influences and the dependence relations between multiple-domain latent factors and latent factors of interest, enforcing acyclicity, sparsity, and elastic net constraints. The resulting optimization thus produces asymptotically correct results. It also exhibits satisfactory capability in regimes of small sample sizes or highly-correlated variables and simultaneously estimates the causal directions and effects between latent factors. Experimental results on both synthetic and real-world data demonstrate the efficacy of our approach.