Causal Discovery with Multi-Domain LiNGAM for Latent Factors

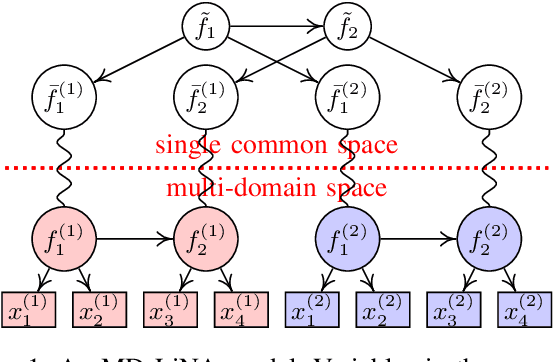
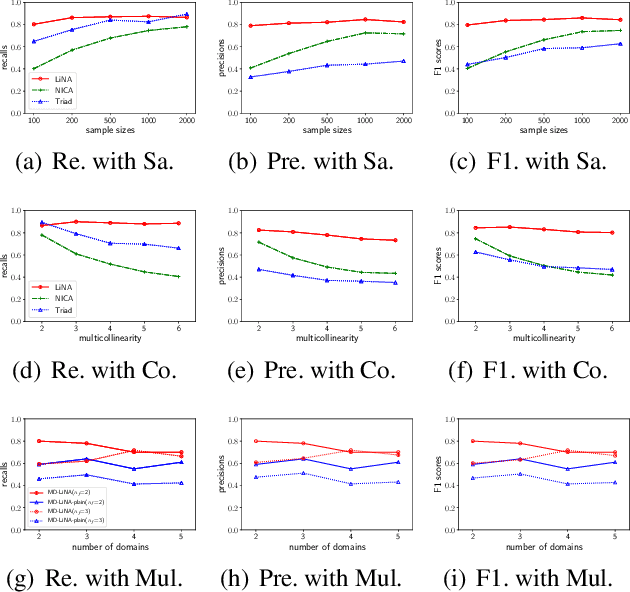
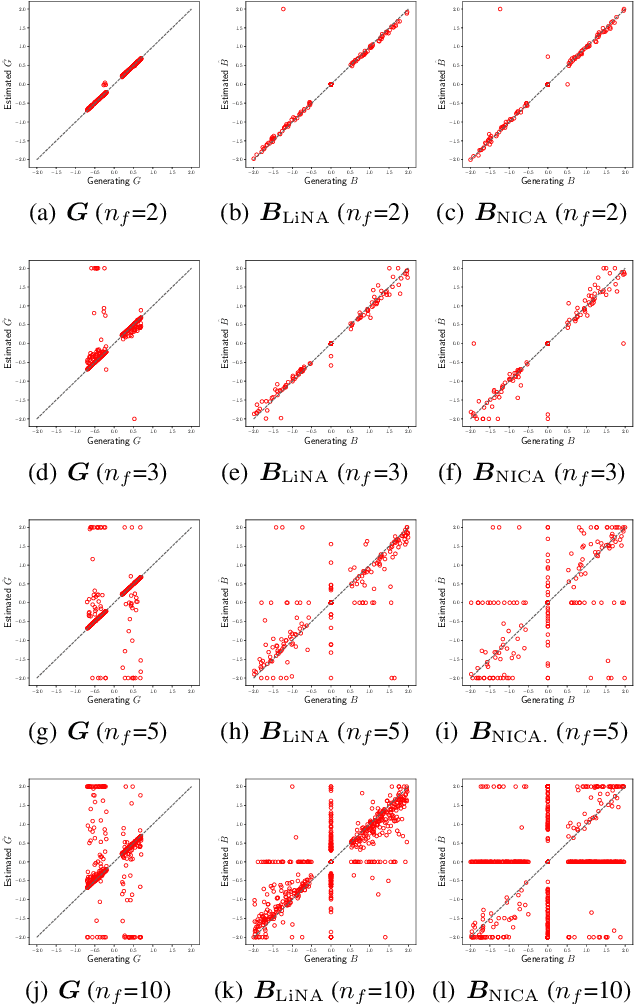
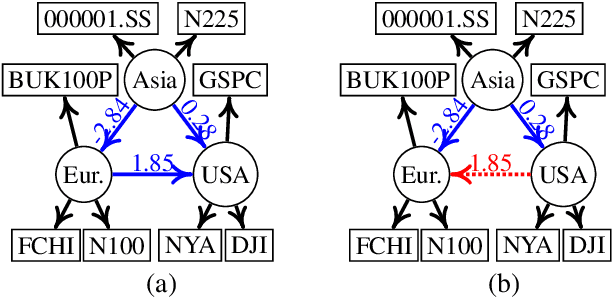
Discovering causal structures among latent factors from observed data is a particularly challenging problem, in which many empirical researchers are interested. Despite its success in certain degrees, existing methods focus on the single-domain observed data only, while in many scenarios data may be originated from distinct domains, e.g. in neuroinformatics. In this paper, we propose Multi-Domain Linear Non-Gaussian Acyclic Models for LAtent Factors (abbreviated as MD-LiNA model) to identify the underlying causal structure between latent factors (of interest), tackling not only single-domain observed data but multiple-domain ones, and provide its identification results. In particular, we first locate the latent factors and estimate the factor loadings matrix for each domain separately. Then to estimate the structure among latent factors (of interest), we derive a score function based on the characterization of independence relations between external influences and the dependence relations between multiple-domain latent factors and latent factors of interest, enforcing acyclicity, sparsity, and elastic net constraints. The resulting optimization thus produces asymptotically correct results. It also exhibits satisfactory capability in regimes of small sample sizes or highly-correlated variables and simultaneously estimates the causal directions and effects between latent factors. Experimental results on both synthetic and real-world data demonstrate the efficacy of our approach.

Sparse estimation via nonconcave penalized likelihood in a factor analysis model

We consider the problem of sparse estimation in a factor analysis model. A traditional estimation procedure in use is the following two-step approach: the model is estimated by maximum likelihood method and then a rotation technique is utilized to find sparse factor loadings. However, the maximum likelihood estimates cannot be obtained when the number of variables is much larger than the number of observations. Furthermore, even if the maximum likelihood estimates are available, the rotation technique does not often produce a sufficiently sparse solution. In order to handle these problems, this paper introduces a penalized likelihood procedure that imposes a nonconvex penalty on the factor loadings. We show that the penalized likelihood procedure can be viewed as a generalization of the traditional two-step approach, and the proposed methodology can produce sparser solutions than the rotation technique. A new algorithm via the EM algorithm along with coordinate descent is introduced to compute the entire solution path, which permits the application to a wide variety of convex and nonconvex penalties. Monte Carlo simulations are conducted to investigate the performance of our modeling strategy. A real data example is also given to illustrate our procedure.