Takashi Nicholas Maeda
Density Ratio-based Causal Discovery from Bivariate Continuous-Discrete Data
May 13, 2025Abstract:This paper proposes a causal discovery method for mixed bivariate data consisting of one continuous and one discrete variable. Existing constraint-based approaches are ineffective in the bivariate setting, as they rely on conditional independence tests that are not suited to bivariate data. Score-based methods either impose strong distributional assumptions or face challenges in fairly comparing causal directions between variables of different types, due to differences in their information content. We introduce a novel approach that determines causal direction by analyzing the monotonicity of the conditional density ratio of the continuous variable, conditioned on different values of the discrete variable. Our theoretical analysis shows that the conditional density ratio exhibits monotonicity when the continuous variable causes the discrete variable, but not in the reverse direction. This property provides a principled basis for comparing causal directions between variables of different types, free from strong distributional assumptions and bias arising from differences in their information content. We demonstrate its effectiveness through experiments on both synthetic and real-world datasets, showing superior accuracy compared to existing methods.
Causal Additive Models with Unobserved Causal Paths and Backdoor Paths
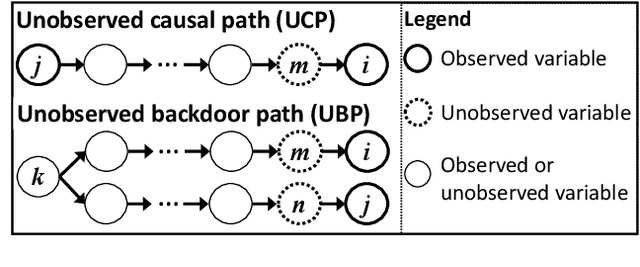
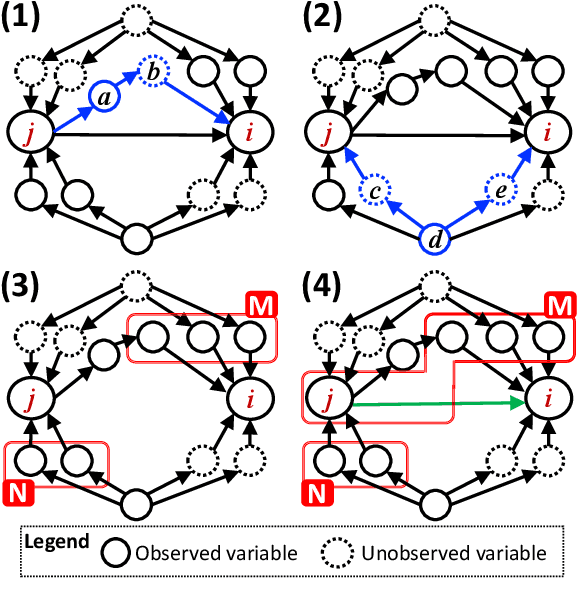
Feb 11, 2025Abstract:Causal additive models have been employed as tractable yet expressive frameworks for causal discovery involving hidden variables. State-of-the-art methodologies suggest that determining the causal relationship between a pair of variables is infeasible in the presence of an unobserved backdoor or an unobserved causal path. Contrary to this assumption, we theoretically show that resolving the causal direction is feasible in certain scenarios by incorporating two novel components into the theory. The first component introduces a novel characterization of regression sets within independence between regression residuals. The second component leverages conditional independence among the observed variables. We also provide a search algorithm that integrates these innovations and demonstrate its competitive performance against existing methods.
Use of Prior Knowledge to Discover Causal Additive Models with Unobserved Variables and its Application to Time Series Data
Jan 18, 2024Abstract:This paper proposes two methods for causal additive models with unobserved variables (CAM-UV). CAM-UV assumes that the causal functions take the form of generalized additive models and that latent confounders are present. First, we propose a method that leverages prior knowledge for efficient causal discovery. Then, we propose an extension of this method for inferring causality in time series data. The original CAM-UV algorithm differs from other existing causal function models in that it does not seek the causal order between observed variables, but rather aims to identify the causes for each observed variable. Therefore, the first proposed method in this paper utilizes prior knowledge, such as understanding that certain variables cannot be causes of specific others. Moreover, by incorporating the prior knowledge that causes precedes their effects in time, we extend the first algorithm to the second method for causal discovery in time series data. We validate the first proposed method by using simulated data to demonstrate that the accuracy of causal discovery increases as more prior knowledge is accumulated. Additionally, we test the second proposed method by comparing it with existing time series causal discovery methods, using both simulated data and real-world data.
Discovery of Causal Additive Models in the Presence of Unobserved Variables
Jun 04, 2021
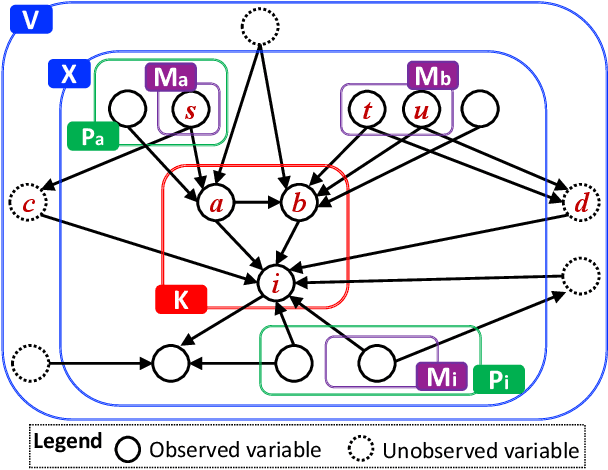
Abstract:Causal discovery from data affected by unobserved variables is an important but difficult problem to solve. The effects that unobserved variables have on the relationships between observed variables are more complex in nonlinear cases than in linear cases. In this study, we focus on causal additive models in the presence of unobserved variables. Causal additive models exhibit structural equations that are additive in the variables and error terms. We take into account the presence of not only unobserved common causes but also unobserved intermediate variables. Our theoretical results show that, when the causal relationships are nonlinear and there are unobserved variables, it is not possible to identify all the causal relationships between observed variables through regression and independence tests. However, our theoretical results also show that it is possible to avoid incorrect inferences. We propose a method to identify all the causal relationships that are theoretically possible to identify without being biased by unobserved variables. The empirical results using artificial data and simulated functional magnetic resonance imaging (fMRI) data show that our method effectively infers causal structures in the presence of unobserved variables.
Causal discovery of linear non-Gaussian acyclic models in the presence of latent confounders
Jan 14, 2020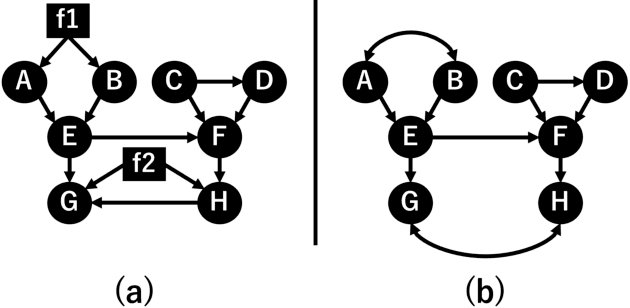
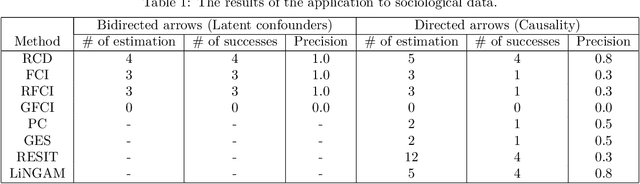

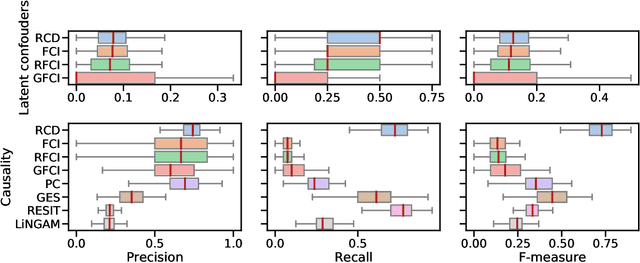
Abstract:Causal discovery from data affected by latent confounders is an important and difficult challenge. Causal functional model-based approaches have not been used to present variables whose relationships are affected by latent confounders, while some constraint-based methods can present them. This paper proposes a causal functional model-based method called repetitive causal discovery (RCD) to discover the causal structure of observed variables affected by latent confounders. RCD repeats inferring the causal directions between a small number of observed variables and determines whether the relationships are affected by latent confounders. RCD finally produces a causal graph where a bi-directed arrow indicates the pair of variables that have the same latent confounders, and a directed arrow indicates the causal direction of a pair of variables that are not affected by the same latent confounder. The results of experimental validation using simulated data and real-world data confirmed that RCD is effective in identifying latent confounders and causal directions between observed variables.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge