A Family of Distributions of Random Subsets for Controlling Positive and Negative Dependence

Positive and negative dependence are fundamental concepts that characterize the attractive and repulsive behavior of random subsets. Although some probabilistic models are known to exhibit positive or negative dependence, it is challenging to seamlessly bridge them with a practicable probabilistic model. In this study, we introduce a new family of distributions, named the discrete kernel point process (DKPP), which includes determinantal point processes and parts of Boltzmann machines. We also develop some computational methods for probabilistic operations and inference with DKPPs, such as calculating marginal and conditional probabilities and learning the parameters. Our numerical experiments demonstrate the controllability of positive and negative dependence and the effectiveness of the computational methods for DKPPs.

Gaussian Process Koopman Mode Decomposition

In this paper, we propose a nonlinear probabilistic generative model of Koopman mode decomposition based on an unsupervised Gaussian process. Existing data-driven methods for Koopman mode decomposition have focused on estimating the quantities specified by Koopman mode decomposition, namely, eigenvalues, eigenfunctions, and modes. Our model enables the simultaneous estimation of these quantities and latent variables governed by an unknown dynamical system. Furthermore, we introduce an efficient strategy to estimate the parameters of our model by low-rank approximations of covariance matrices. Applying the proposed model to both synthetic data and a real-world epidemiological dataset, we show that various analyses are available using the estimated parameters.

Bayesian Sparse Covariance Structure Analysis for Correlated Count Data

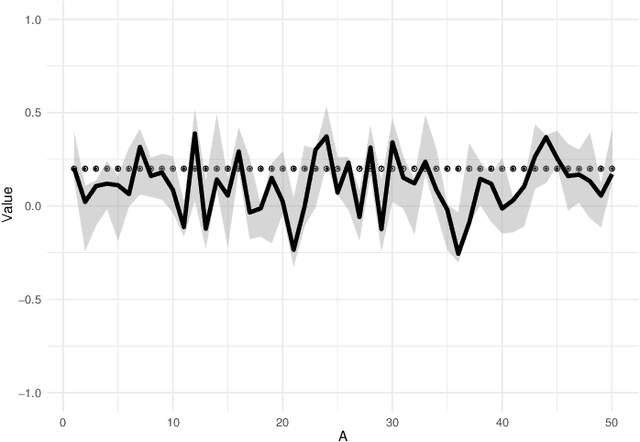
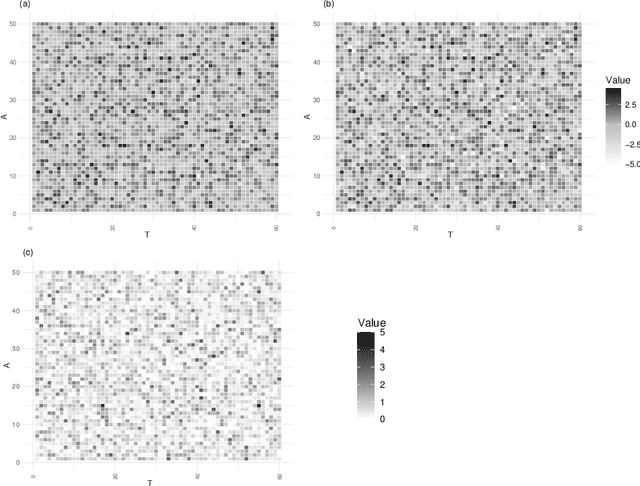
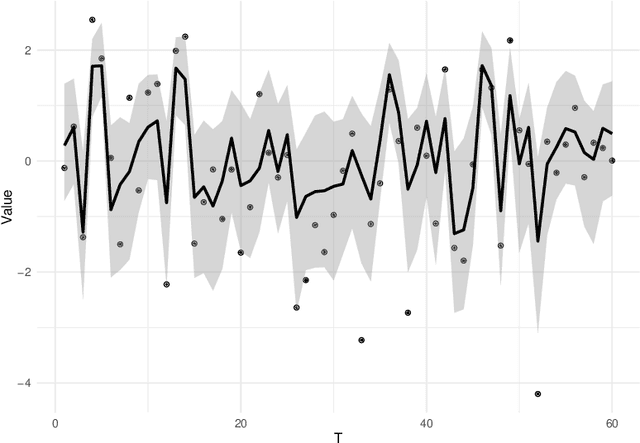
In this paper, we propose a Bayesian Graphical LASSO for correlated countable data and apply it to spatial crime data. In the proposed model, we assume a Gaussian Graphical Model for the latent variables which dominate the potential risks of crimes. To evaluate the proposed model, we determine optimal hyperparameters which represent samples better. We apply the proposed model for estimation of the sparse inverse covariance of the latent variable and evaluate the partial correlation coefficients. Finally, we illustrate the results on crime spots data and consider the estimated latent variables and the partial correlation coefficients of the sparse inverse covariance.

Fast Bayesian Restoration of Poisson Corrupted Images with INLA

Photon-limited images are often seen in fields such as medical imaging. Although the number of collected photons on an image sensor statistically follows Poisson distribution, this type of noise is intractable, unlike Gaussian noise. In this study, we propose a Bayesian restoration method of Poisson corrupted image using Integrated Nested Laplace Approximation (INLA), which is a computational method to evaluate marginalized posterior distributions of latent Gaussian models (LGMs). When the original image can be regarded as ICAR (intrinsic conditional auto-regressive) model reasonably, our method performs very faster than well-known ones such as loopy belief propagation-based method and Markov chain Monte Carlo (MCMC) without decreasing the accuracy.