Optimistic Natural Policy Gradient: a Simple Efficient Policy Optimization Framework for Online RL
Paper and Code
May 18, 2023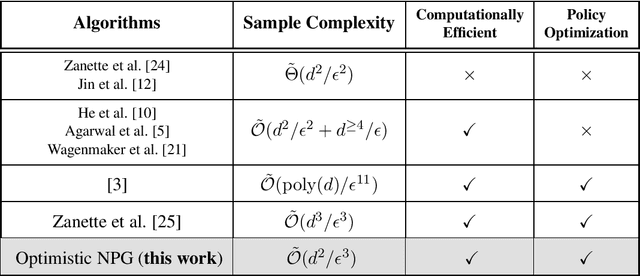
While policy optimization algorithms have played an important role in recent empirical success of Reinforcement Learning (RL), the existing theoretical understanding of policy optimization remains rather limited -- they are either restricted to tabular MDPs or suffer from highly suboptimal sample complexity, especial in online RL where exploration is necessary. This paper proposes a simple efficient policy optimization framework -- Optimistic NPG for online RL. Optimistic NPG can be viewed as simply combining of the classic natural policy gradient (NPG) algorithm [Kakade, 2001] with optimistic policy evaluation subroutines to encourage exploration. For $d$-dimensional linear MDPs, Optimistic NPG is computationally efficient, and learns an $\varepsilon$-optimal policy within $\tilde{O}(d^2/\varepsilon^3)$ samples, which is the first computationally efficient algorithm whose sample complexity has the optimal dimension dependence $\tilde{\Theta}(d^2)$. It also improves over state-of-the-art results of policy optimization algorithms [Zanette et al., 2021] by a factor of $d$. For general function approximation that subsumes linear MDPs, Optimistic NPG, to our best knowledge, is also the first policy optimization algorithm that achieves the polynomial sample complexity for learning near-optimal policies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge