Faster Gaussian Processes via Deep Embeddings

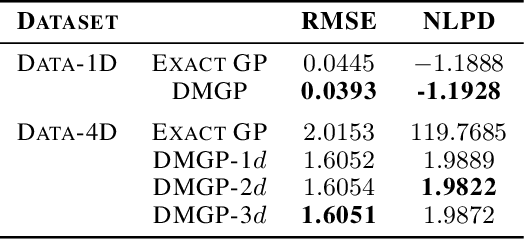
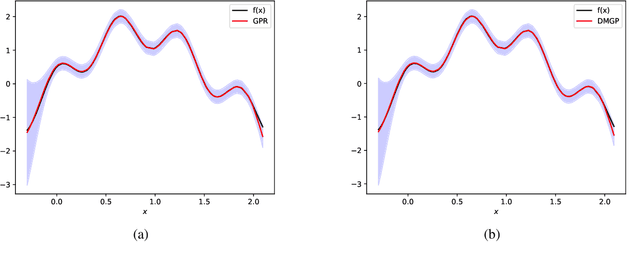
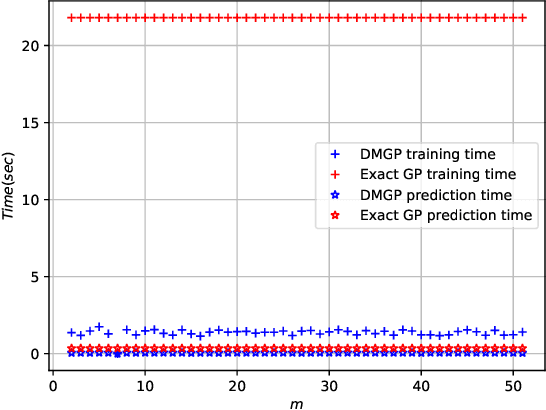
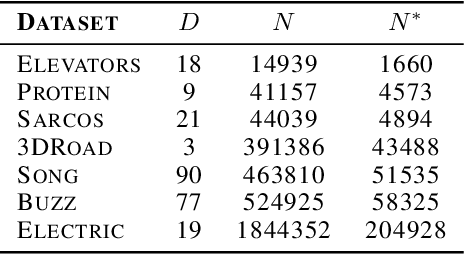
Gaussian processes provide a probabilistic framework for quantifying uncertainty of prediction and have been adopted in many applications in Statistics and Bayesian optimization. Unfortunately, they are hard to scale to large datasets as they necessitate inverting matrices whose size is linear in the number of observations. Moreover, they necessitate an a priori chosen functional form for their kernels with predetermined features. Our contribution is a framework that addresses both challenges. We use deep neural networks for automatic feature extraction, combined with explicit functional forms for the eigenspectrum of Gaussian processes with Gaussian kernels, to derive a Gaussian process inference and prediction framework whose complexity scales linearly in the number of observations and which accommodates automatic feature extraction. On a series of datasets, our method outperforms state of the art scalable Gaussian process approximations.