Learning multi-modal generative models with permutation-invariant encoders and tighter variational bounds

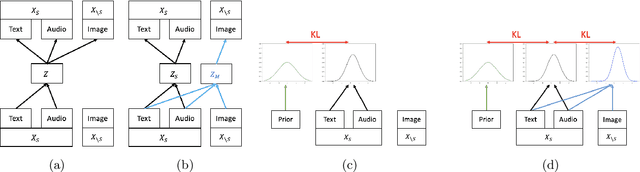
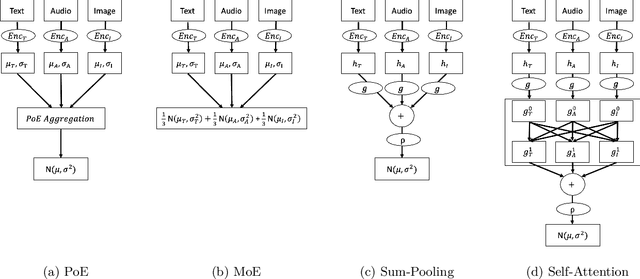
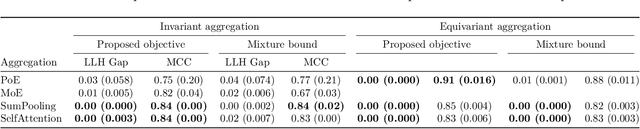
Devising deep latent variable models for multi-modal data has been a long-standing theme in machine learning research. Multi-modal Variational Autoencoders (VAEs) have been a popular generative model class that learns latent representations which jointly explain multiple modalities. Various objective functions for such models have been suggested, often motivated as lower bounds on the multi-modal data log-likelihood or from information-theoretic considerations. In order to encode latent variables from different modality subsets, Product-of-Experts (PoE) or Mixture-of-Experts (MoE) aggregation schemes have been routinely used and shown to yield different trade-offs, for instance, regarding their generative quality or consistency across multiple modalities. In this work, we consider a variational bound that can tightly lower bound the data log-likelihood. We develop more flexible aggregation schemes that generalise PoE or MoE approaches by combining encoded features from different modalities based on permutation-invariant neural networks. Our numerical experiments illustrate trade-offs for multi-modal variational bounds and various aggregation schemes. We show that tighter variational bounds and more flexible aggregation models can become beneficial when one wants to approximate the true joint distribution over observed modalities and latent variables in identifiable models.

Learning variational autoencoders via MCMC speed measures

Variational autoencoders (VAEs) are popular likelihood-based generative models which can be efficiently trained by maximizing an Evidence Lower Bound (ELBO). There has been much progress in improving the expressiveness of the variational distribution to obtain tighter variational bounds and increased generative performance. Whilst previous work has leveraged Markov chain Monte Carlo (MCMC) methods for the construction of variational densities, gradient-based methods for adapting the proposal distributions for deep latent variable models have received less attention. This work suggests an entropy-based adaptation for a short-run Metropolis-adjusted Langevin (MALA) or Hamiltonian Monte Carlo (HMC) chain while optimising a tighter variational bound to the log-evidence. Experiments show that this approach yields higher held-out log-likelihoods as well as improved generative metrics. Our implicit variational density can adapt to complicated posterior geometries of latent hierarchical representations arising in hierarchical VAEs.

Entropy-based adaptive Hamiltonian Monte Carlo

Hamiltonian Monte Carlo (HMC) is a popular Markov Chain Monte Carlo (MCMC) algorithm to sample from an unnormalized probability distribution. A leapfrog integrator is commonly used to implement HMC in practice, but its performance can be sensitive to the choice of mass matrix used therein. We develop a gradient-based algorithm that allows for the adaptation of the mass matrix by encouraging the leapfrog integrator to have high acceptance rates while also exploring all dimensions jointly. In contrast to previous work that adapt the hyperparameters of HMC using some form of expected squared jumping distance, the adaptation strategy suggested here aims to increase sampling efficiency by maximizing an approximation of the proposal entropy. We illustrate that using multiple gradients in the HMC proposal can be beneficial compared to a single gradient-step in Metropolis-adjusted Langevin proposals. Empirical evidence suggests that the adaptation method can outperform different versions of HMC schemes by adjusting the mass matrix to the geometry of the target distribution and by providing some control on the integration time.

Copula-like Variational Inference

This paper considers a new family of variational distributions motivated by Sklar's theorem. This family is based on new copula-like densities on the hypercube with non-uniform marginals which can be sampled efficiently, i.e. with a complexity linear in the dimension of state space. Then, the proposed variational densities that we suggest can be seen as arising from these copula-like densities used as base distributions on the hypercube with Gaussian quantile functions and sparse rotation matrices as normalizing flows. The latter correspond to a rotation of the marginals with complexity $\mathcal{O}(d \log d)$. We provide some empirical evidence that such a variational family can also approximate non-Gaussian posteriors and can be beneficial compared to Gaussian approximations. Our method performs largely comparably to state-of-the-art variational approximations on standard regression and classification benchmarks for Bayesian Neural Networks.

Scalable Bayesian Learning for State Space Models using Variational Inference with SMC Samplers

We present a scalable approach to performing approximate fully Bayesian inference in generic state space models. The proposed method is an alternative to particle MCMC that provides fully Bayesian inference of both the dynamic latent states and the static parameters of the model. We build up on recent advances in computational statistics that combine variational methods with sequential Monte Carlo sampling and we demonstrate the advantages of performing full Bayesian inference over the static parameters rather than just performing variational EM approximations. We illustrate how our approach enables scalable inference in multivariate stochastic volatility models and self-exciting point process models that allow for flexible dynamics in the latent intensity function.