Fully Scalable Gaussian Processes using Subspace Inducing Inputs

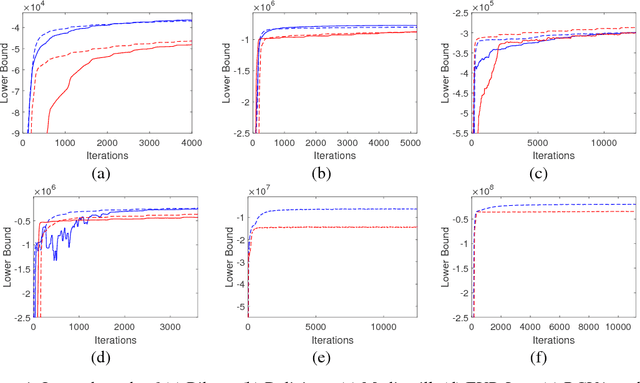
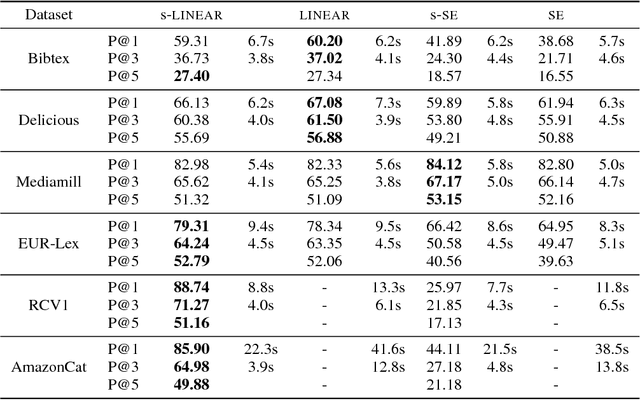
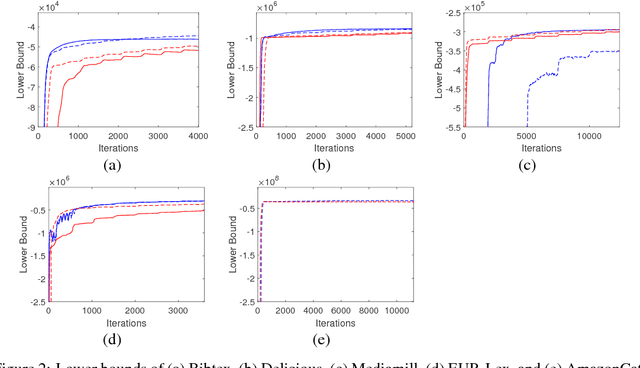
We introduce fully scalable Gaussian processes, an implementation scheme that tackles the problem of treating a high number of training instances together with high dimensional input data. Our key idea is a representation trick over the inducing variables called subspace inducing inputs. This is combined with certain matrix-preconditioning based parametrizations of the variational distributions that lead to simplified and numerically stable variational lower bounds. Our illustrative applications are based on challenging extreme multi-label classification problems with the extra burden of the very large number of class labels. We demonstrate the usefulness of our approach by presenting predictive performances together with low computational times in datasets with extremely large number of instances and input dimensions.