Differentially private partitioned variational inference

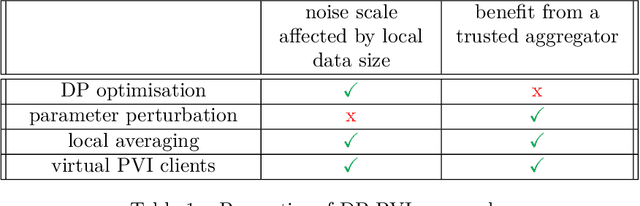
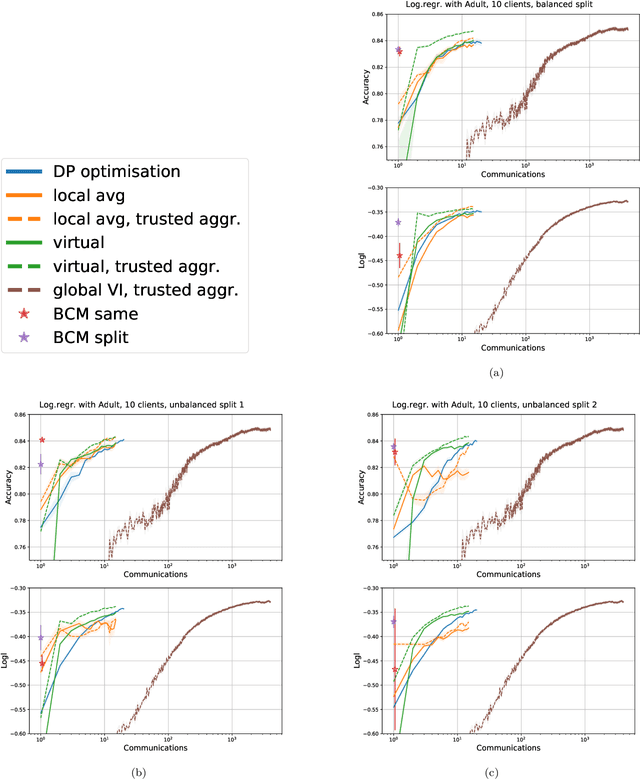
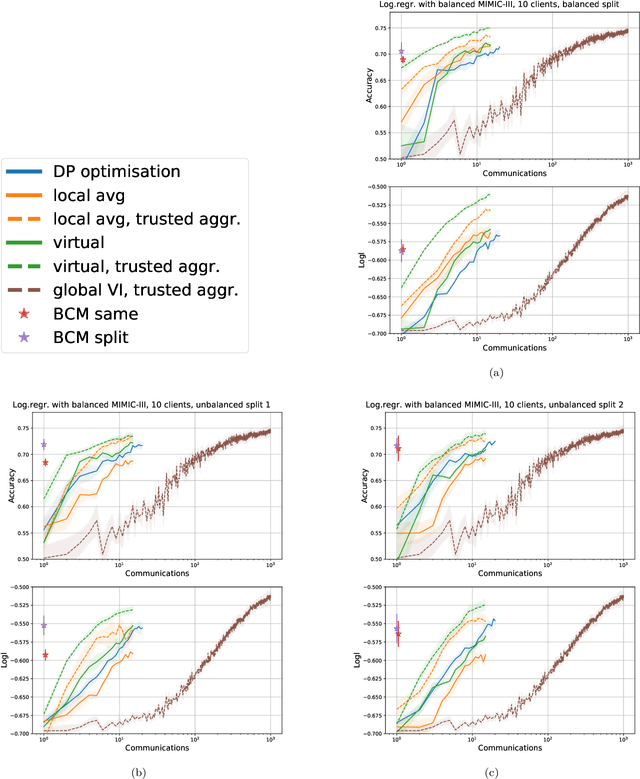
Learning a privacy-preserving model from distributed sensitive data is an increasingly important problem, often formulated in the federated learning context. Variational inference has recently been extended to the non-private federated learning setting via the partitioned variational inference algorithm. For privacy protection, the current gold standard is called differential privacy. Differential privacy guarantees privacy in a strong, mathematically clearly defined sense. In this paper, we present differentially private partitioned variational inference, the first general framework for learning a variational approximation to a Bayesian posterior distribution in the federated learning setting while minimising the number of communication rounds and providing differential privacy guarantees for data subjects. We propose three alternative implementations in the general framework, one based on perturbing local optimisation done by individual parties, and two based on perturbing global updates (one using a version of federated averaging, one adding virtual parties to the protocol), and compare their properties both theoretically and empirically. We show that perturbing the local optimisation works well with simple and complex models as long as each party has enough local data. However, the privacy is always guaranteed independently by each party. In contrast, perturbing the global updates works best with relatively simple models. Given access to suitable secure primitives, such as secure aggregation or secure shuffling, the performance can be improved by all parties guaranteeing privacy jointly.