Time-Causal VAE: Robust Financial Time Series Generator

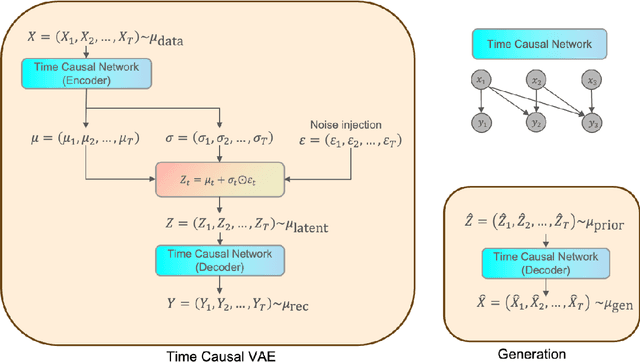
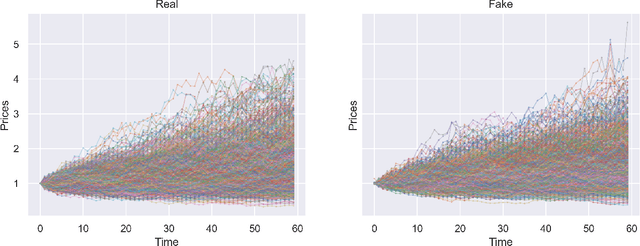
We build a time-causal variational autoencoder (TC-VAE) for robust generation of financial time series data. Our approach imposes a causality constraint on the encoder and decoder networks, ensuring a causal transport from the real market time series to the fake generated time series. Specifically, we prove that the TC-VAE loss provides an upper bound on the causal Wasserstein distance between market distributions and generated distributions. Consequently, the TC-VAE loss controls the discrepancy between optimal values of various dynamic stochastic optimization problems under real and generated distributions. To further enhance the model's ability to approximate the latent representation of the real market distribution, we integrate a RealNVP prior into the TC-VAE framework. Finally, extensive numerical experiments show that TC-VAE achieves promising results on both synthetic and real market data. This is done by comparing real and generated distributions according to various statistical distances, demonstrating the effectiveness of the generated data for downstream financial optimization tasks, as well as showcasing that the generated data reproduces stylized facts of real financial market data.

Metric Hypertransformers are Universal Adapted Maps

We introduce a universal class of geometric deep learning models, called metric hypertransformers (MHTs), capable of approximating any adapted map $F:\mathscr{X}^{\mathbb{Z}}\rightarrow \mathscr{Y}^{\mathbb{Z}}$ with approximable complexity, where $\mathscr{X}\subseteq \mathbb{R}^d$ and $\mathscr{Y}$ is any suitable metric space, and $\mathscr{X}^{\mathbb{Z}}$ (resp. $\mathscr{Y}^{\mathbb{Z}}$) capture all discrete-time paths on $\mathscr{X}$ (resp. $\mathscr{Y}$). Suitable spaces $\mathscr{Y}$ include various (adapted) Wasserstein spaces, all Fr\'{e}chet spaces admitting a Schauder basis, and a variety of Riemannian manifolds arising from information geometry. Even in the static case, where $f:\mathscr{X}\rightarrow \mathscr{Y}$ is a H\"{o}lder map, our results provide the first (quantitative) universal approximation theorem compatible with any such $\mathscr{X}$ and $\mathscr{Y}$. Our universal approximation theorems are quantitative, and they depend on the regularity of $F$, the choice of activation function, the metric entropy and diameter of $\mathscr{X}$, and on the regularity of the compact set of paths whereon the approximation is performed. Our guiding examples originate from mathematical finance. Notably, the MHT models introduced here are able to approximate a broad range of stochastic processes' kernels, including solutions to SDEs, many processes with arbitrarily long memory, and functions mapping sequential data to sequences of forward rate curves.

SPATE-GAN: Improved Generative Modeling of Dynamic Spatio-Temporal Patterns with an Autoregressive Embedding Loss

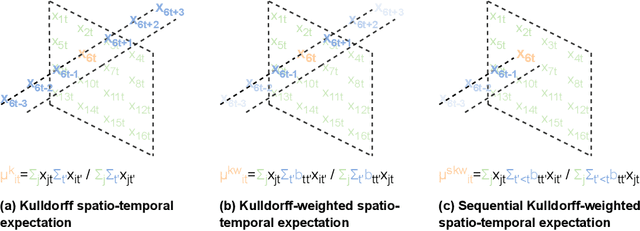
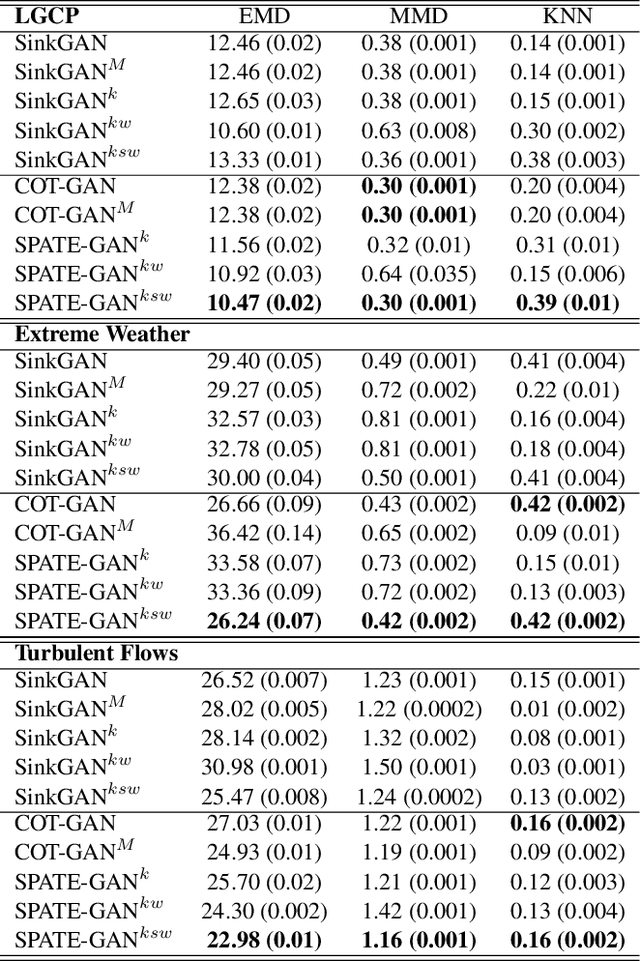
From ecology to atmospheric sciences, many academic disciplines deal with data characterized by intricate spatio-temporal complexities, the modeling of which often requires specialized approaches. Generative models of these data are of particular interest, as they enable a range of impactful downstream applications like simulation or creating synthetic training data. Recent work has highlighted the potential of generative adversarial nets (GANs) for generating spatio-temporal data. A new GAN algorithm COT-GAN, inspired by the theory of causal optimal transport (COT), was proposed in an attempt to better tackle this challenge. However, the task of learning more complex spatio-temporal patterns requires additional knowledge of their specific data structures. In this study, we propose a novel loss objective combined with COT-GAN based on an autoregressive embedding to reinforce the learning of spatio-temporal dynamics. We devise SPATE (spatio-temporal association), a new metric measuring spatio-temporal autocorrelation by using the deviance of observations from their expected values. We compute SPATE for real and synthetic data samples and use it to compute an embedding loss that considers space-time interactions, nudging the GAN to learn outputs that are faithful to the observed dynamics. We test this new objective on a diverse set of complex spatio-temporal patterns: turbulent flows, log-Gaussian Cox processes and global weather data. We show that our novel embedding loss improves performance without any changes to the architecture of the COT-GAN backbone, highlighting our model's increased capacity for capturing autoregressive structures. We also contextualize our work with respect to recent advances in physics-informed deep learning and interdisciplinary work connecting neural networks with geographic and geophysical sciences.

Quantized Conditional COT-GAN for Video Prediction

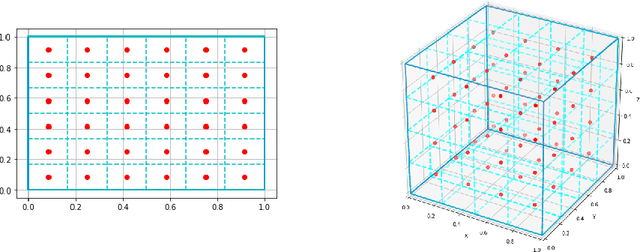
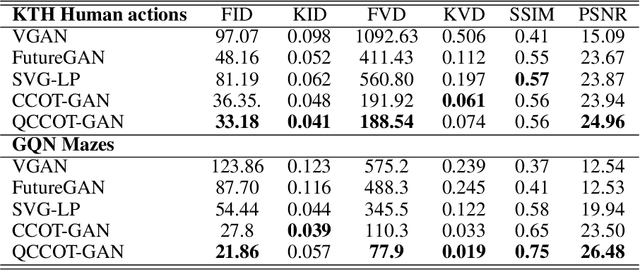
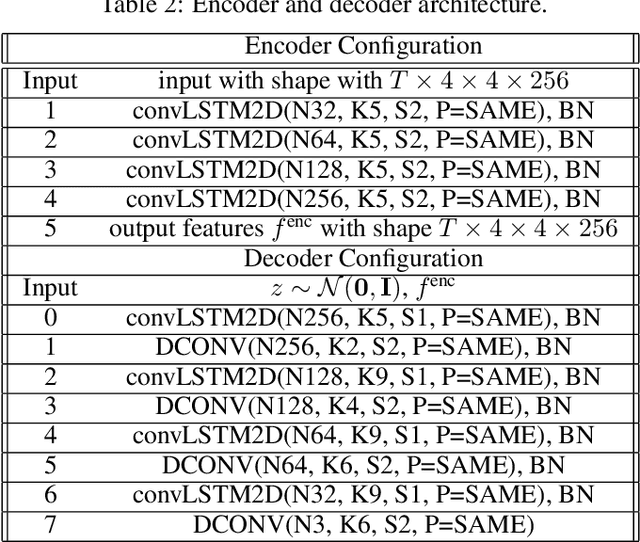
Causal Optimal Transport (COT) results from imposing a temporal causality constraint on classic optimal transport problems, which naturally generates a new concept of distances between distributions on path spaces. The first application of the COT theory for sequential learning was given in Xu et al. (2020), where COT-GAN was introduced as an adversarial algorithm to train implicit generative models optimized for producing sequential data. Relying on Xu et al. (2020), the contribution of the present paper is twofold. First, we develop a conditional version of COT-GAN suitable for sequence prediction. This means that the dataset is now used in order to learn how a sequence will evolve given the observation of its past evolution. Second, we improve on the convergence results by working with modifications of the empirical measures via a specific type of quantization due to Backhoff et al. (2020). The resulting quantized conditional COT-GAN algorithm is illustrated with an application for video prediction.

COT-GAN: Generating Sequential Data via Causal Optimal Transport

We introduce COT-GAN, an adversarial algorithm to train implicit generative models optimized for producing sequential data. The loss function of this algorithm is formulated using ideas from Causal Optimal Transport (COT), which combines classic optimal transport methods with an additional temporal causality constraint. Remarkably, we find that this causality condition provides a natural framework to parameterize the cost function that is learned by the discriminator as a robust (worst-case) distance, and an ideal mechanism for learning time dependent data distributions. Following Genevay et al.\ (2018), we also include an entropic penalization term which allows for the use of the Sinkhorn algorithm when computing the optimal transport cost. Our experiments show effectiveness and stability of COT-GAN when generating both low- and high-dimensional time series data. The success of the algorithm also relies on a new, improved version of the Sinkhorn divergence which demonstrates less bias in learning.