Daniel B. Neill
New York University
Learning Representational Disparities
May 23, 2025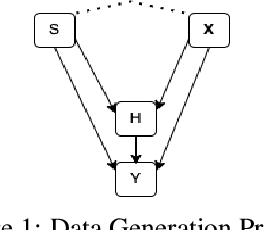
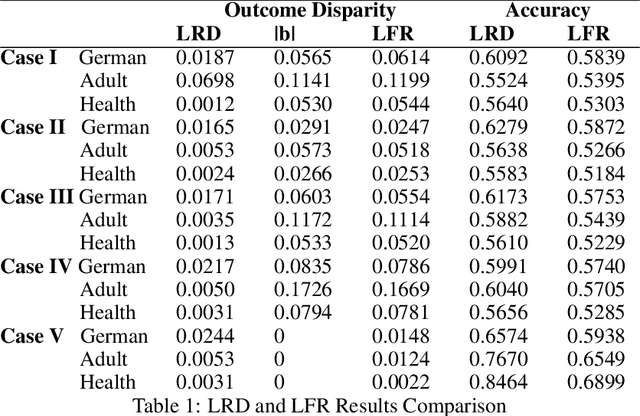
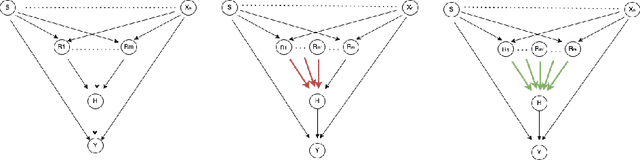
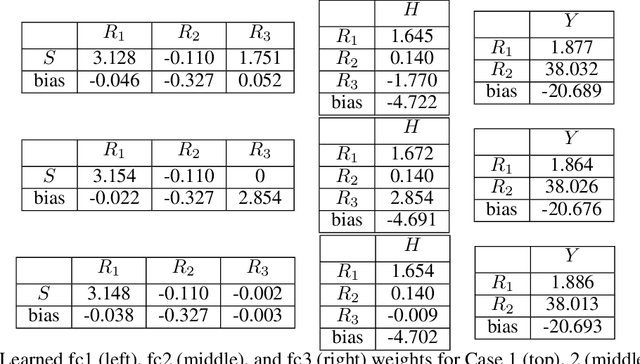
Abstract:We propose a fair machine learning algorithm to model interpretable differences between observed and desired human decision-making, with the latter aimed at reducing disparity in a downstream outcome impacted by the human decision. Prior work learns fair representations without considering the outcome in the decision-making process. We model the outcome disparities as arising due to the different representations of the input seen by the observed and desired decision-maker, which we term representational disparities. Our goal is to learn interpretable representational disparities which could potentially be corrected by specific nudges to the human decision, mitigating disparities in the downstream outcome; we frame this as a multi-objective optimization problem using a neural network. Under reasonable simplifying assumptions, we prove that our neural network model of the representational disparity learns interpretable weights that fully mitigate the outcome disparity. We validate objectives and interpret results using real-world German Credit, Adult, and Heritage Health datasets.
Be Intentional About Fairness!: Fairness, Size, and Multiplicity in the Rashomon Set
Jan 26, 2025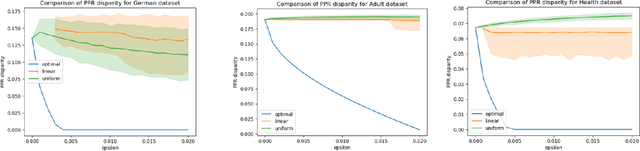
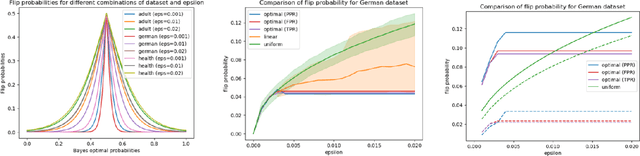
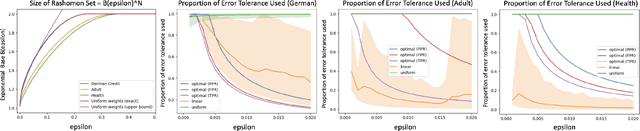
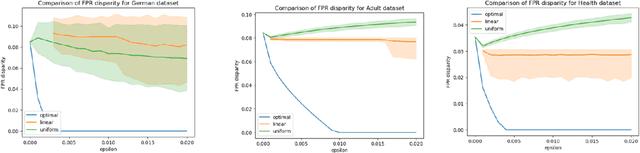
Abstract:When selecting a model from a set of equally performant models, how much unfairness can you really reduce? Is it important to be intentional about fairness when choosing among this set, or is arbitrarily choosing among the set of ''good'' models good enough? Recent work has highlighted that the phenomenon of model multiplicity-where multiple models with nearly identical predictive accuracy exist for the same task-has both positive and negative implications for fairness, from strengthening the enforcement of civil rights law in AI systems to showcasing arbitrariness in AI decision-making. Despite the enormous implications of model multiplicity, there is little work that explores the properties of sets of equally accurate models, or Rashomon sets, in general. In this paper, we present five main theoretical and methodological contributions which help us to understand the relatively unexplored properties of the Rashomon set, in particular with regards to fairness. Our contributions include methods for efficiently sampling models from this set and techniques for identifying the fairest models according to key fairness metrics such as statistical parity. We also derive the probability that an individual's prediction will be flipped within the Rashomon set, as well as expressions for the set's size and the distribution of error tolerance used across models. These results lead to policy-relevant takeaways, such as the importance of intentionally looking for fair models within the Rashomon set, and understanding which individuals or groups may be more susceptible to arbitrary decisions.
Auditing Predictive Models for Intersectional Biases
Jun 22, 2023

Abstract:Predictive models that satisfy group fairness criteria in aggregate for members of a protected class, but do not guarantee subgroup fairness, could produce biased predictions for individuals at the intersection of two or more protected classes. To address this risk, we propose Conditional Bias Scan (CBS), a flexible auditing framework for detecting intersectional biases in classification models. CBS identifies the subgroup for which there is the most significant bias against the protected class, as compared to the equivalent subgroup in the non-protected class, and can incorporate multiple commonly used fairness definitions for both probabilistic and binarized predictions. We show that this methodology can detect previously unidentified intersectional and contextual biases in the COMPAS pre-trial risk assessment tool and has higher bias detection power compared to similar methods that audit for subgroup fairness.
Insufficiently Justified Disparate Impact: A New Criterion for Subgroup Fairness
Jun 19, 2023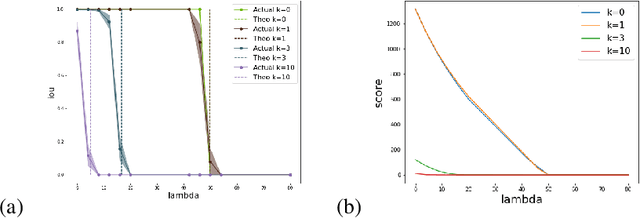

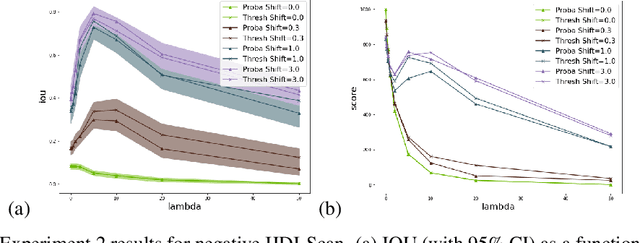

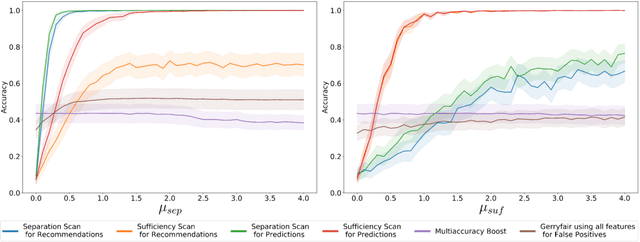
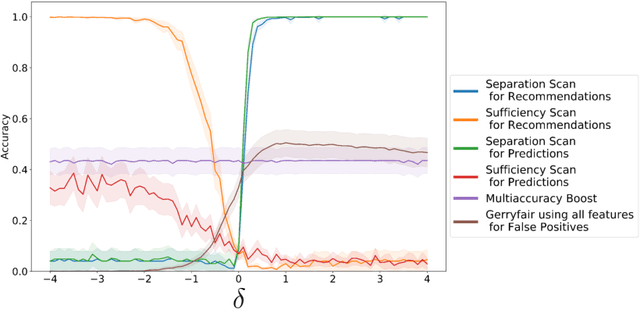
Abstract:In this paper, we develop a new criterion, "insufficiently justified disparate impact" (IJDI), for assessing whether recommendations (binarized predictions) made by an algorithmic decision support tool are fair. Our novel, utility-based IJDI criterion evaluates false positive and false negative error rate imbalances, identifying statistically significant disparities between groups which are present even when adjusting for group-level differences in base rates. We describe a novel IJDI-Scan approach which can efficiently identify the intersectional subpopulations, defined across multiple observed attributes of the data, with the most significant IJDI. To evaluate IJDI-Scan's performance, we conduct experiments on both simulated and real-world data, including recidivism risk assessment and credit scoring. Further, we implement and evaluate approaches to mitigating IJDI for the detected subpopulations in these domains.
Provable Detection of Propagating Sampling Bias in Prediction Models
Feb 13, 2023Abstract:With an increased focus on incorporating fairness in machine learning models, it becomes imperative not only to assess and mitigate bias at each stage of the machine learning pipeline but also to understand the downstream impacts of bias across stages. Here we consider a general, but realistic, scenario in which a predictive model is learned from (potentially biased) training data, and model predictions are assessed post-hoc for fairness by some auditing method. We provide a theoretical analysis of how a specific form of data bias, differential sampling bias, propagates from the data stage to the prediction stage. Unlike prior work, we evaluate the downstream impacts of data biases quantitatively rather than qualitatively and prove theoretical guarantees for detection. Under reasonable assumptions, we quantify how the amount of bias in the model predictions varies as a function of the amount of differential sampling bias in the data, and at what point this bias becomes provably detectable by the auditor. Through experiments on two criminal justice datasets -- the well-known COMPAS dataset and historical data from NYPD's stop and frisk policy -- we demonstrate that the theoretical results hold in practice even when our assumptions are relaxed.
Calibrated Nonparametric Scan Statistics for Anomalous Pattern Detection in Graphs
Jun 26, 2022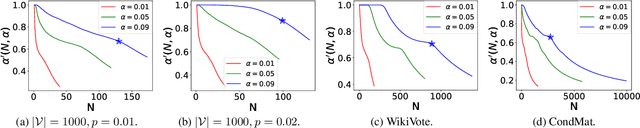
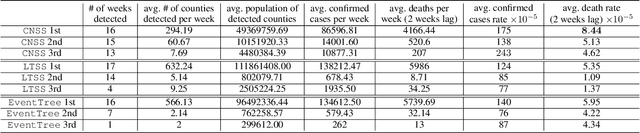
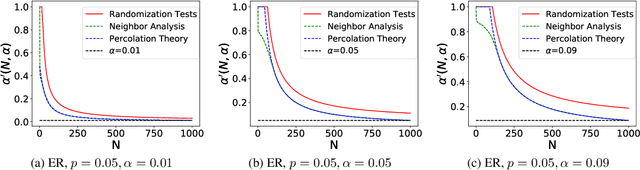

Abstract:We propose a new approach, the calibrated nonparametric scan statistic (CNSS), for more accurate detection of anomalous patterns in large-scale, real-world graphs. Scan statistics identify connected subgraphs that are interesting or unexpected through maximization of a likelihood ratio statistic; in particular, nonparametric scan statistics (NPSSs) identify subgraphs with a higher than expected proportion of individually significant nodes. However, we show that recently proposed NPSS methods are miscalibrated, failing to account for the maximization of the statistic over the multiplicity of subgraphs. This results in both reduced detection power for subtle signals, and low precision of the detected subgraph even for stronger signals. Thus we develop a new statistical approach to recalibrate NPSSs, correctly adjusting for multiple hypothesis testing and taking the underlying graph structure into account. While the recalibration, based on randomization testing, is computationally expensive, we propose both an efficient (approximate) algorithm and new, closed-form lower bounds (on the expected maximum proportion of significant nodes for subgraphs of a given size, under the null hypothesis of no anomalous patterns). These advances, along with the integration of recent core-tree decomposition methods, enable CNSS to scale to large real-world graphs, with substantial improvement in the accuracy of detected subgraphs. Extensive experiments on both semi-synthetic and real-world datasets are demonstrated to validate the effectiveness of our proposed methods, in comparison with state-of-the-art counterparts.
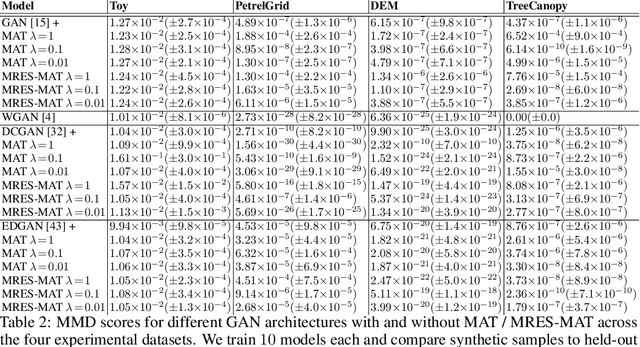
SPATE-GAN: Improved Generative Modeling of Dynamic Spatio-Temporal Patterns with an Autoregressive Embedding Loss
Sep 30, 2021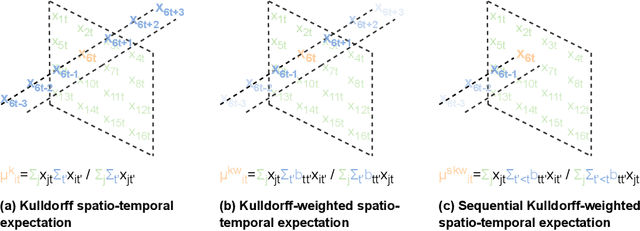
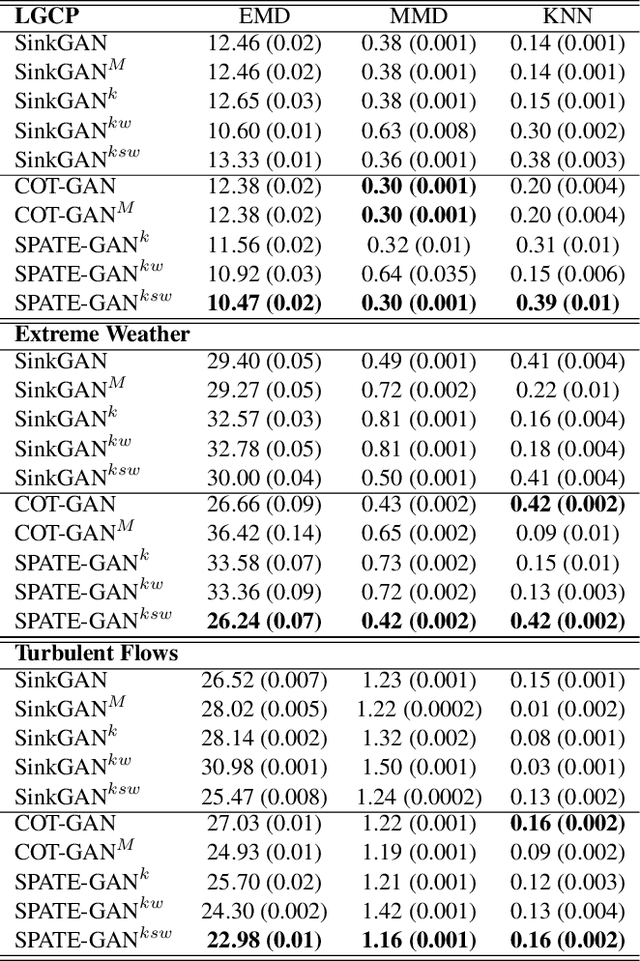

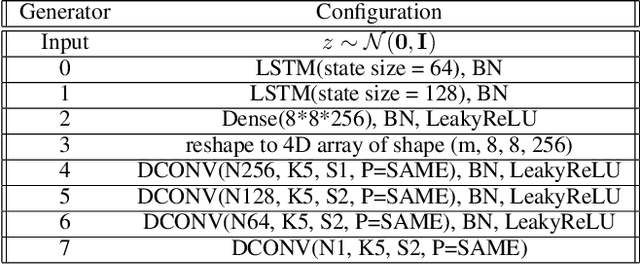
Abstract:From ecology to atmospheric sciences, many academic disciplines deal with data characterized by intricate spatio-temporal complexities, the modeling of which often requires specialized approaches. Generative models of these data are of particular interest, as they enable a range of impactful downstream applications like simulation or creating synthetic training data. Recent work has highlighted the potential of generative adversarial nets (GANs) for generating spatio-temporal data. A new GAN algorithm COT-GAN, inspired by the theory of causal optimal transport (COT), was proposed in an attempt to better tackle this challenge. However, the task of learning more complex spatio-temporal patterns requires additional knowledge of their specific data structures. In this study, we propose a novel loss objective combined with COT-GAN based on an autoregressive embedding to reinforce the learning of spatio-temporal dynamics. We devise SPATE (spatio-temporal association), a new metric measuring spatio-temporal autocorrelation by using the deviance of observations from their expected values. We compute SPATE for real and synthetic data samples and use it to compute an embedding loss that considers space-time interactions, nudging the GAN to learn outputs that are faithful to the observed dynamics. We test this new objective on a diverse set of complex spatio-temporal patterns: turbulent flows, log-Gaussian Cox processes and global weather data. We show that our novel embedding loss improves performance without any changes to the architecture of the COT-GAN backbone, highlighting our model's increased capacity for capturing autoregressive structures. We also contextualize our work with respect to recent advances in physics-informed deep learning and interdisciplinary work connecting neural networks with geographic and geophysical sciences.
Policing Chronic and Temporary Hot Spots of Violent Crime: A Controlled Field Experiment
Nov 11, 2020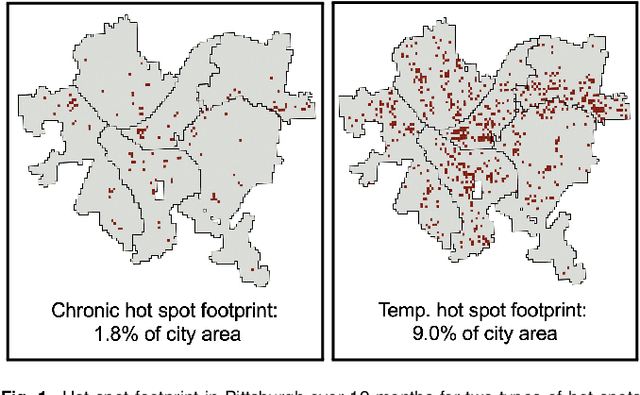
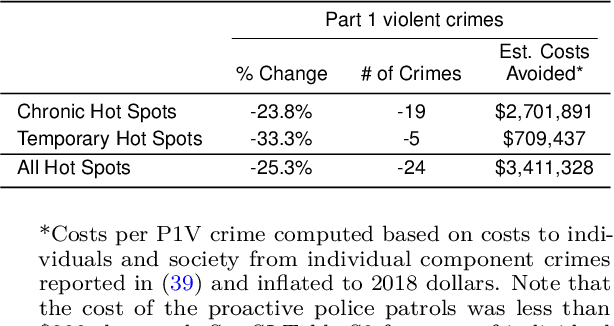
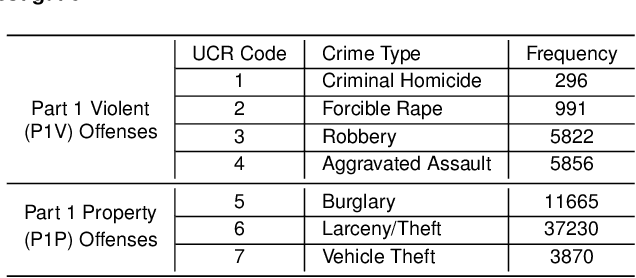
Abstract:Hot-spot-based policing programs aim to deter crime through increased proactive patrols at high-crime locations. While most hot spot programs target easily identified chronic hot spots, we introduce models for predicting temporary hot spots to address effectiveness and equity objectives for crime prevention, and present findings from a crossover experiment evaluating application of hot spot predictions to prevent serious violent crime in Pittsburgh, PA. Over a 12-month experimental period, the Pittsburgh Bureau of Police assigned uniformed patrol officers to weekly predicted chronic and temporary hot spots of serious violent crimes comprising 0.5 percent of the city's area. We find statistically and practically significant reductions in serious violent crime counts within treatment hot spots as compared to control hot spots, with an overall reduction of 25.3 percent in the FBI-classified Part 1 Violent (P1V) crimes of homicide, rape, robbery, and aggravated assault, and a 39.7 percent reduction of African-American and other non-white victims of P1V crimes. We find that temporary hot spots increase spatial dispersion of patrols and have a greater percentage reduction in P1V crimes than chronic hot spots but fewer total number of crimes prevented. Only foot patrols, not car patrols, had statistically significant crime reductions in hot spots. We find no evidence of crime displacement; instead, we find weakly statistically significant spillover of crime prevention benefits to adjacent areas. In addition, we find no evidence that the community-oriented hot spot patrols produced over-policing arrests of minority or other populations.
SXL: Spatially explicit learning of geographic processes with auxiliary tasks
Jun 18, 2020
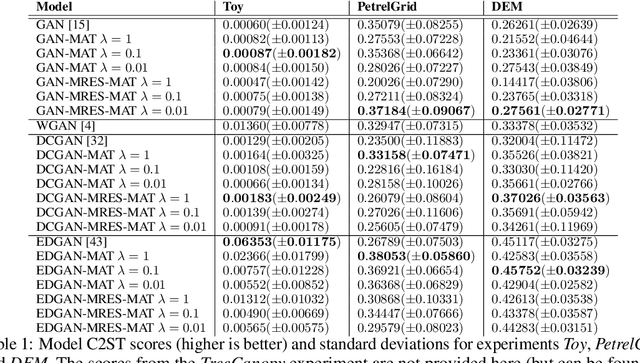
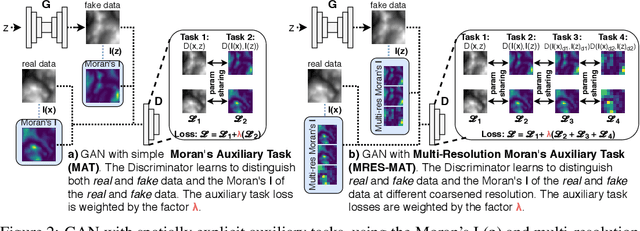
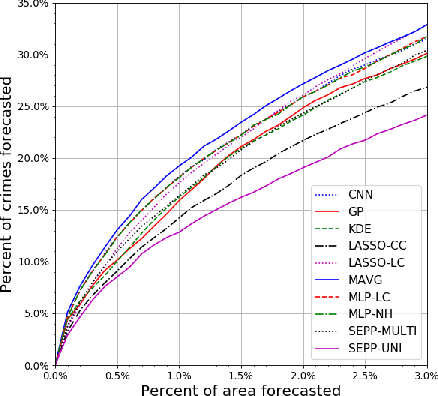
Abstract:From earth system sciences to climate modeling and ecology, many of the greatest empirical modeling challenges are geographic in nature. As these processes are characterized by spatial dynamics, we can exploit their autoregressive nature to inform learning algorithms. We introduce SXL, a method for learning with geospatial data using explicitly spatial auxiliary tasks. We embed the local Moran's I, a well-established measure of local spatial autocorrelation, into the training process, "nudging" the model to learn the direction and magnitude of local autoregressive effects in parallel with the primary task. Further, we propose an expansion of Moran's I to multiple resolutions to capture effects at different spatial granularities and over varying distance scales. We show the superiority of this method for training deep neural networks using experiments with real-world geospatial data in both generative and predictive modeling tasks. Our approach can be used with arbitrary network architectures and, in our experiments, consistently improves their performance. We also outperform appropriate, domain-specific interpolation benchmarks. Our work highlights how integrating the geographic information sciences and spatial statistics into machine learning models can address the specific challenges of spatial data.
Change Surfaces for Expressive Multidimensional Changepoints and Counterfactual Prediction
Oct 30, 2018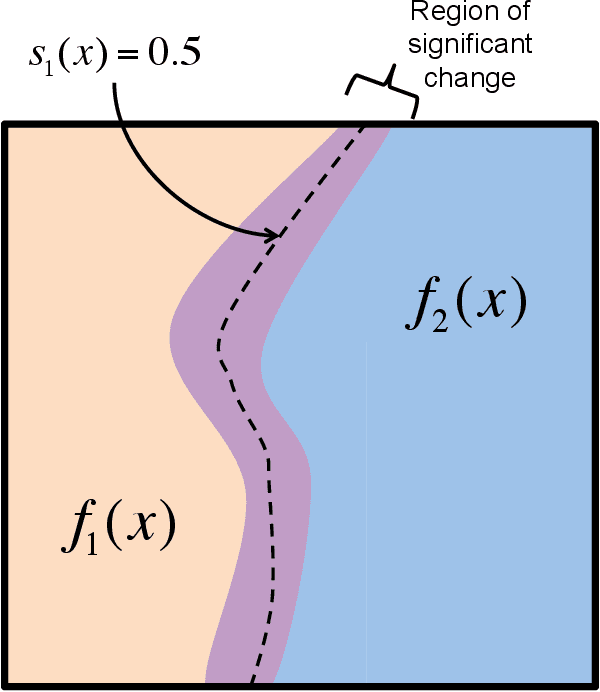

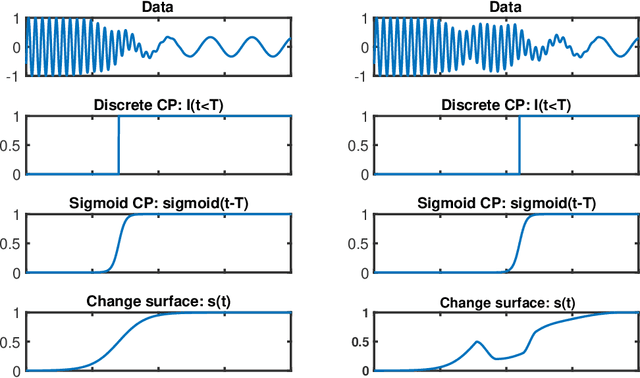
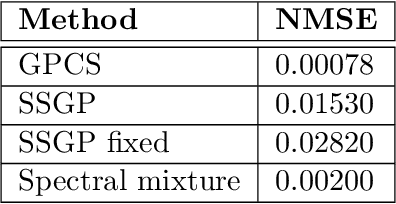
Abstract:Identifying changes in model parameters is fundamental in machine learning and statistics. However, standard changepoint models are limited in expressiveness, often addressing unidimensional problems and assuming instantaneous changes. We introduce change surfaces as a multidimensional and highly expressive generalization of changepoints. We provide a model-agnostic formalization of change surfaces, illustrating how they can provide variable, heterogeneous, and non-monotonic rates of change across multiple dimensions. Additionally, we show how change surfaces can be used for counterfactual prediction. As a concrete instantiation of the change surface framework, we develop Gaussian Process Change Surfaces (GPCS). We demonstrate counterfactual prediction with Bayesian posterior mean and credible sets, as well as massive scalability by introducing novel methods for additive non-separable kernels. Using two large spatio-temporal datasets we employ GPCS to discover and characterize complex changes that can provide scientific and policy relevant insights. Specifically, we analyze twentieth century measles incidence across the United States and discover previously unknown heterogeneous changes after the introduction of the measles vaccine. Additionally, we apply the model to requests for lead testing kits in New York City, discovering distinct spatial and demographic patterns.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge