Transition-Aware Multi-Activity Knowledge Tracing

Accurate modeling of student knowledge is essential for large-scale online learning systems that are increasingly used for student training. Knowledge tracing aims to model student knowledge state given the student's sequence of learning activities. Modern Knowledge tracing (KT) is usually formulated as a supervised sequence learning problem to predict students' future practice performance according to their past observed practice scores by summarizing student knowledge state as a set of evolving hidden variables. Because of this formulation, many current KT solutions are not fit for modeling student learning from non-assessed learning activities with no explicit feedback or score observation (e.g., watching video lectures that are not graded). Additionally, these models cannot explicitly represent the dynamics of knowledge transfer among different learning activities, particularly between the assessed (e.g., quizzes) and non-assessed (e.g., video lectures) learning activities. In this paper, we propose Transition-Aware Multi-activity Knowledge Tracing (TAMKOT), which models knowledge transfer between learning materials, in addition to student knowledge, when students transition between and within assessed and non-assessed learning materials. TAMKOT is formulated as a deep recurrent multi-activity learning model that explicitly learns knowledge transfer by activating and learning a set of knowledge transfer matrices, one for each transition type between student activities. Accordingly, our model allows for representing each material type in a different yet transferrable latent space while maintaining student knowledge in a shared space. We evaluate our model on three real-world publicly available datasets and demonstrate TAMKOT's capability in predicting student performance and modeling knowledge transfer.

Block-Structured Optimization for Subgraph Detection in Interdependent Networks

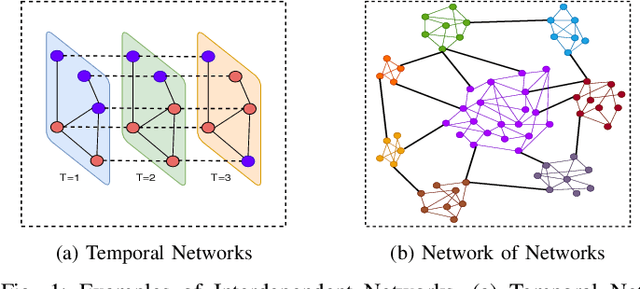
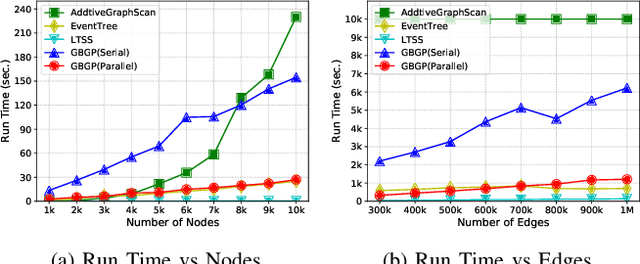
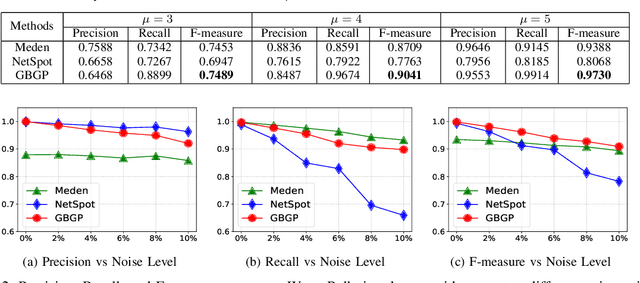
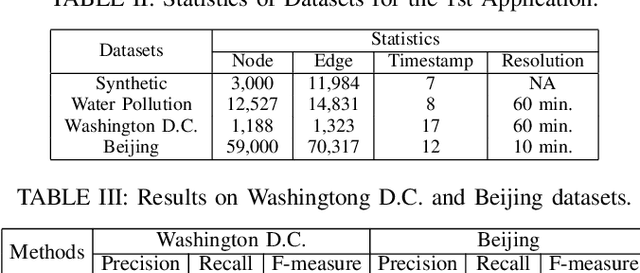
We propose a generalized framework for block-structured nonconvex optimization, which can be applied to structured subgraph detection in interdependent networks, such as multi-layer networks, temporal networks, networks of networks, and many others. Specifically, we design an effective, efficient, and parallelizable projection algorithm, namely Graph Block-structured Gradient Projection (GBGP), to optimize a general non-linear function subject to graph-structured constraints. We prove that our algorithm: 1) runs in nearly-linear time on the network size; 2) enjoys a theoretical approximation guarantee. Moreover, we demonstrate how our framework can be applied to two very practical applications and conduct comprehensive experiments to show the effectiveness and efficiency of our proposed algorithm.

Calibrated Nonparametric Scan Statistics for Anomalous Pattern Detection in Graphs

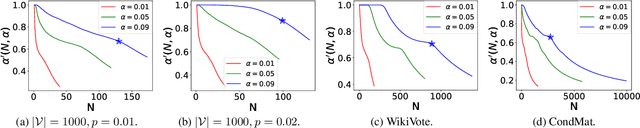
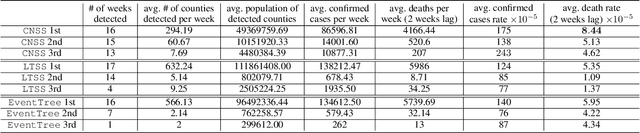
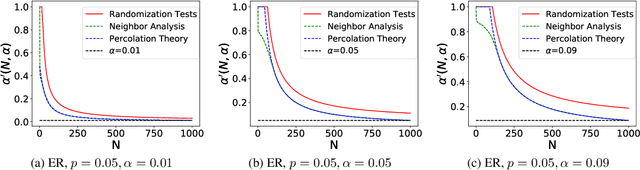
We propose a new approach, the calibrated nonparametric scan statistic (CNSS), for more accurate detection of anomalous patterns in large-scale, real-world graphs. Scan statistics identify connected subgraphs that are interesting or unexpected through maximization of a likelihood ratio statistic; in particular, nonparametric scan statistics (NPSSs) identify subgraphs with a higher than expected proportion of individually significant nodes. However, we show that recently proposed NPSS methods are miscalibrated, failing to account for the maximization of the statistic over the multiplicity of subgraphs. This results in both reduced detection power for subtle signals, and low precision of the detected subgraph even for stronger signals. Thus we develop a new statistical approach to recalibrate NPSSs, correctly adjusting for multiple hypothesis testing and taking the underlying graph structure into account. While the recalibration, based on randomization testing, is computationally expensive, we propose both an efficient (approximate) algorithm and new, closed-form lower bounds (on the expected maximum proportion of significant nodes for subgraphs of a given size, under the null hypothesis of no anomalous patterns). These advances, along with the integration of recent core-tree decomposition methods, enable CNSS to scale to large real-world graphs, with substantial improvement in the accuracy of detected subgraphs. Extensive experiments on both semi-synthetic and real-world datasets are demonstrated to validate the effectiveness of our proposed methods, in comparison with state-of-the-art counterparts.

Modeling Knowledge Acquisition from Multiple Learning Resource Types

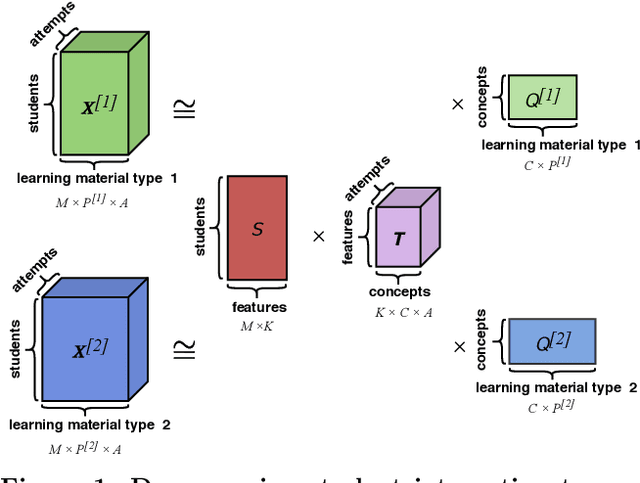
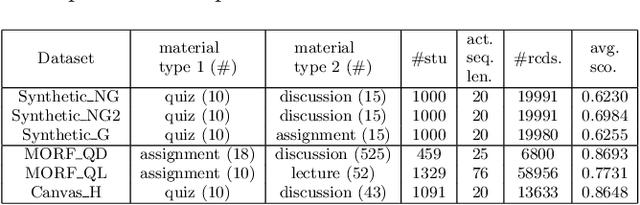
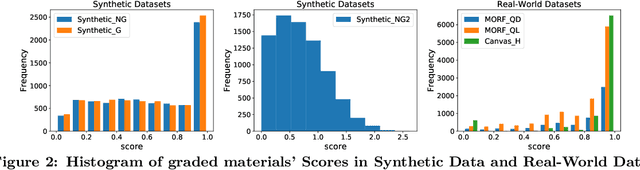
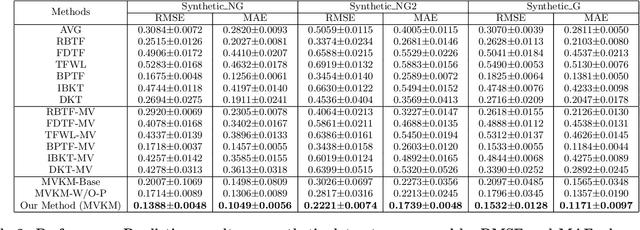
Students acquire knowledge as they interact with a variety of learning materials, such as video lectures, problems, and discussions. Modeling student knowledge at each point during their learning period and understanding the contribution of each learning material to student knowledge are essential for detecting students' knowledge gaps and recommending learning materials to them. Current student knowledge modeling techniques mostly rely on one type of learning material, mainly problems, to model student knowledge growth. These approaches ignore the fact that students also learn from other types of material. In this paper, we propose a student knowledge model that can capture knowledge growth as a result of learning from a diverse set of learning resource types while unveiling the association between the learning materials of different types. Our multi-view knowledge model (MVKM) incorporates a flexible knowledge increase objective on top of a multi-view tensor factorization to capture occasional forgetting while representing student knowledge and learning material concepts in a lower-dimensional latent space. We evaluate our model in different experiments toshow that it can accurately predict students' future performance, differentiate between knowledge gain in different student groups and concepts, and unveil hidden similarities across learning materials of different types.