Pavan Ravishankar
Learning Representational Disparities
May 23, 2025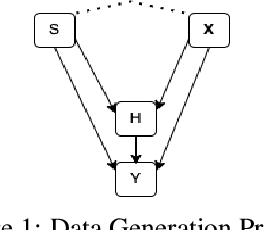
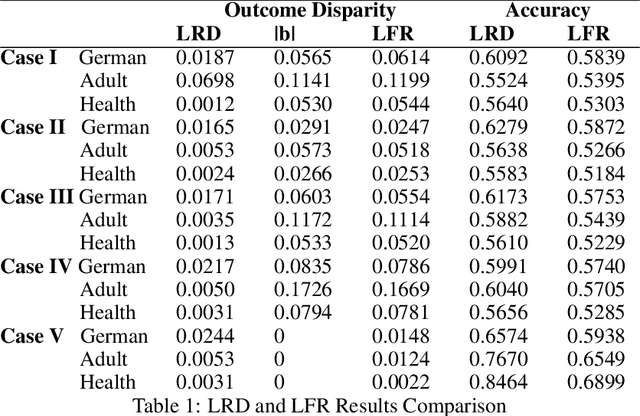
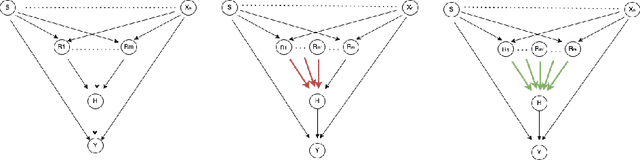
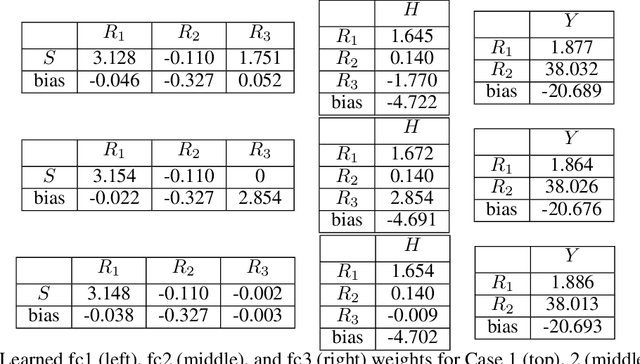
Abstract:We propose a fair machine learning algorithm to model interpretable differences between observed and desired human decision-making, with the latter aimed at reducing disparity in a downstream outcome impacted by the human decision. Prior work learns fair representations without considering the outcome in the decision-making process. We model the outcome disparities as arising due to the different representations of the input seen by the observed and desired decision-maker, which we term representational disparities. Our goal is to learn interpretable representational disparities which could potentially be corrected by specific nudges to the human decision, mitigating disparities in the downstream outcome; we frame this as a multi-objective optimization problem using a neural network. Under reasonable simplifying assumptions, we prove that our neural network model of the representational disparity learns interpretable weights that fully mitigate the outcome disparity. We validate objectives and interpret results using real-world German Credit, Adult, and Heritage Health datasets.
Be Intentional About Fairness!: Fairness, Size, and Multiplicity in the Rashomon Set
Jan 26, 2025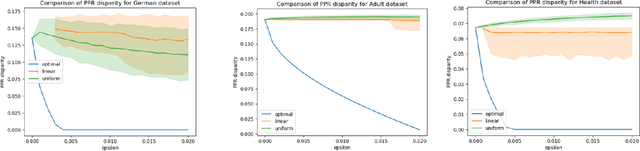
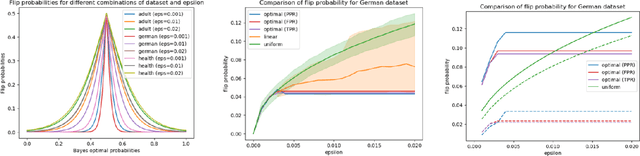
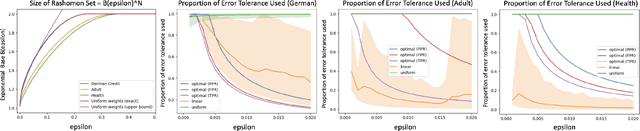
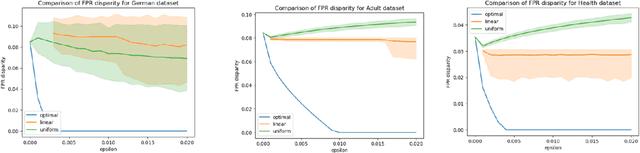
Abstract:When selecting a model from a set of equally performant models, how much unfairness can you really reduce? Is it important to be intentional about fairness when choosing among this set, or is arbitrarily choosing among the set of ''good'' models good enough? Recent work has highlighted that the phenomenon of model multiplicity-where multiple models with nearly identical predictive accuracy exist for the same task-has both positive and negative implications for fairness, from strengthening the enforcement of civil rights law in AI systems to showcasing arbitrariness in AI decision-making. Despite the enormous implications of model multiplicity, there is little work that explores the properties of sets of equally accurate models, or Rashomon sets, in general. In this paper, we present five main theoretical and methodological contributions which help us to understand the relatively unexplored properties of the Rashomon set, in particular with regards to fairness. Our contributions include methods for efficiently sampling models from this set and techniques for identifying the fairest models according to key fairness metrics such as statistical parity. We also derive the probability that an individual's prediction will be flipped within the Rashomon set, as well as expressions for the set's size and the distribution of error tolerance used across models. These results lead to policy-relevant takeaways, such as the importance of intentionally looking for fair models within the Rashomon set, and understanding which individuals or groups may be more susceptible to arbitrary decisions.
Provable Detection of Propagating Sampling Bias in Prediction Models
Feb 13, 2023Abstract:With an increased focus on incorporating fairness in machine learning models, it becomes imperative not only to assess and mitigate bias at each stage of the machine learning pipeline but also to understand the downstream impacts of bias across stages. Here we consider a general, but realistic, scenario in which a predictive model is learned from (potentially biased) training data, and model predictions are assessed post-hoc for fairness by some auditing method. We provide a theoretical analysis of how a specific form of data bias, differential sampling bias, propagates from the data stage to the prediction stage. Unlike prior work, we evaluate the downstream impacts of data biases quantitatively rather than qualitatively and prove theoretical guarantees for detection. Under reasonable assumptions, we quantify how the amount of bias in the model predictions varies as a function of the amount of differential sampling bias in the data, and at what point this bias becomes provably detectable by the auditor. Through experiments on two criminal justice datasets -- the well-known COMPAS dataset and historical data from NYPD's stop and frisk policy -- we demonstrate that the theoretical results hold in practice even when our assumptions are relaxed.
A Causal Approach for Unfair Edge Prioritization and Discrimination Removal
Nov 29, 2021
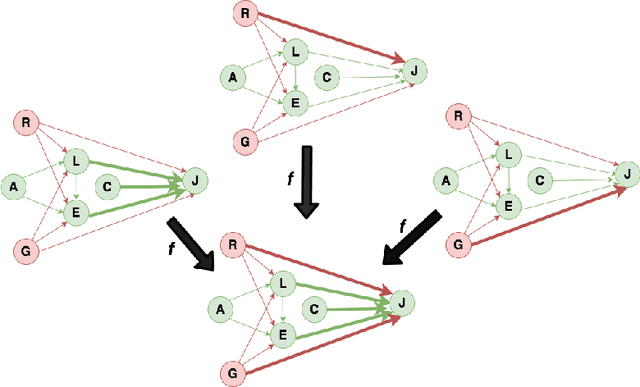
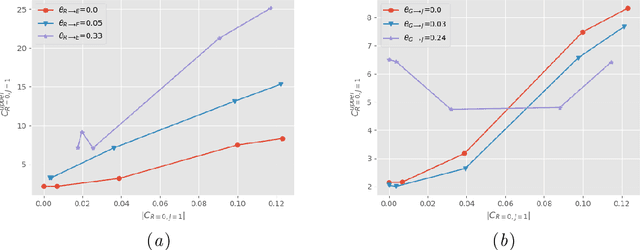
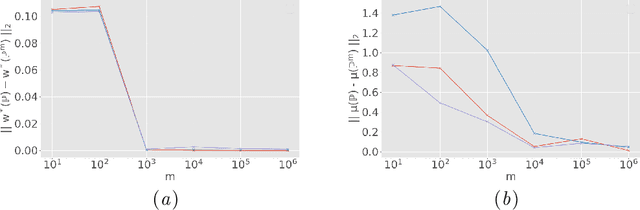
Abstract:In budget-constrained settings aimed at mitigating unfairness, like law enforcement, it is essential to prioritize the sources of unfairness before taking measures to mitigate them in the real world. Unlike previous works, which only serve as a caution against possible discrimination and de-bias data after data generation, this work provides a toolkit to mitigate unfairness during data generation, given by the Unfair Edge Prioritization algorithm, in addition to de-biasing data after generation, given by the Discrimination Removal algorithm. We assume that a non-parametric Markovian causal model representative of the data generation procedure is given. The edges emanating from the sensitive nodes in the causal graph, such as race, are assumed to be the sources of unfairness. We first quantify Edge Flow in any edge X -> Y, which is the belief of observing a specific value of Y due to the influence of a specific value of X along X -> Y. We then quantify Edge Unfairness by formulating a non-parametric model in terms of edge flows. We then prove that cumulative unfairness towards sensitive groups in a decision, like race in a bail decision, is non-existent when edge unfairness is absent. We prove this result for the non-trivial non-parametric model setting when the cumulative unfairness cannot be expressed in terms of edge unfairness. We then measure the Potential to mitigate the Cumulative Unfairness when edge unfairness is decreased. Based on these measurements, we propose the Unfair Edge Prioritization algorithm that can then be used by policymakers. We also propose the Discrimination Removal Procedure that de-biases a data distribution by eliminating optimization constraints that grow exponentially in the number of sensitive attributes and values taken by them. Extensive experiments validate the theorem and specifications used for quantifying the above measures.
A Causal Linear Model to Quantify Edge Unfairness for Unfair Edge Prioritization and Discrimination Removal
Jul 16, 2020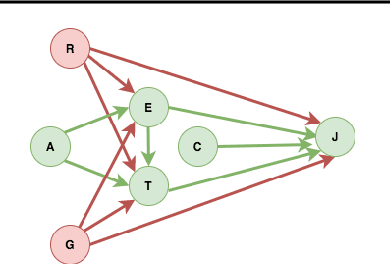
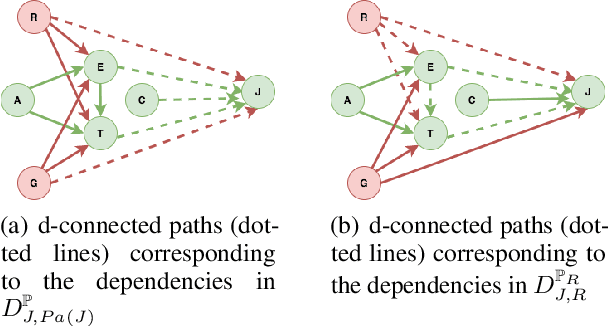
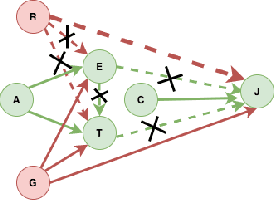
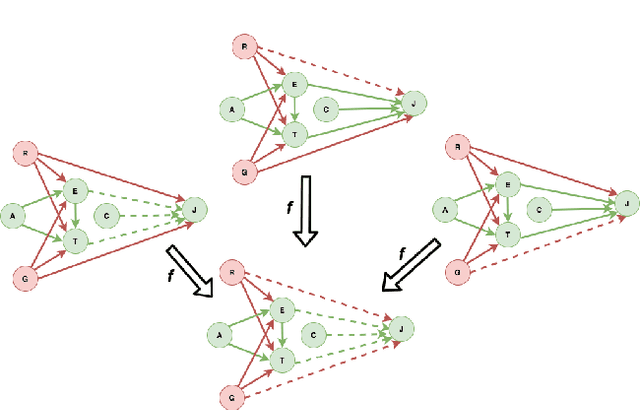
Abstract:The dataset can be generated by an unfair mechanism in numerous settings. For instance, a judicial system is unfair if it rejects the bail plea of an accused based on the race. To mitigate the unfairness in the procedure generating the dataset, we need to know and quantify where the unfairness is originating from, how it affects the overall unfairness, and how to prioritize these sources of unfairness to address the real-world issues underlying these sources. Prior work of (Zhang, et al., 2017) identifies and removes discrimination after data is generated but does not suggest a methodology to mitigate unfairness in the data generation phase. We use the notion of an unfair edge, same as (Chiappa, et al., 2018), to be a source of discrimination and quantify unfairness along an unfair edge. We also quantify overall unfairness in a particular decision towards a subset of sensitive attributes in terms of edge unfairness and measure the sensitivity of the former when the latter is varied. Using the formulation of cumulative unfairness in terms of edge unfairness, we alter the discrimination removal methodology discussed in (Zhang, et al., 2017) by not formulating it as an optimization problem. This helps in getting rid of constraints that grow exponentially in the number of sensitive attributes and values taken by them. Finally, we discuss a priority algorithm for policymakers to address the real-world issues underlying the edges that result in unfairness. The experimental section validates the linear model assumption made to quantify edge unfairness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge