Blindness of score-based methods to isolated components and mixing proportions

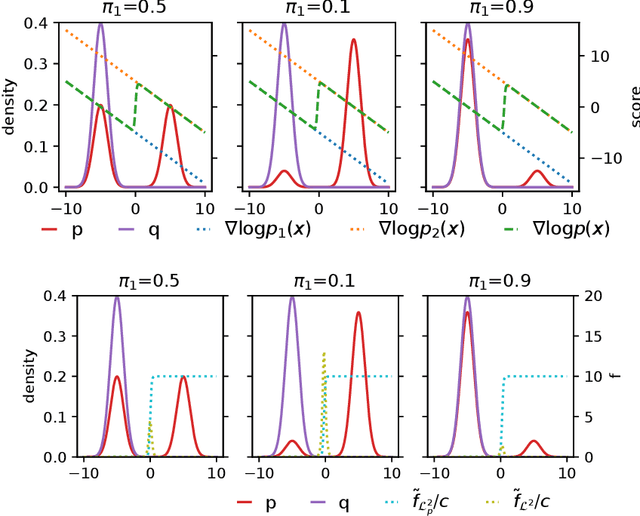
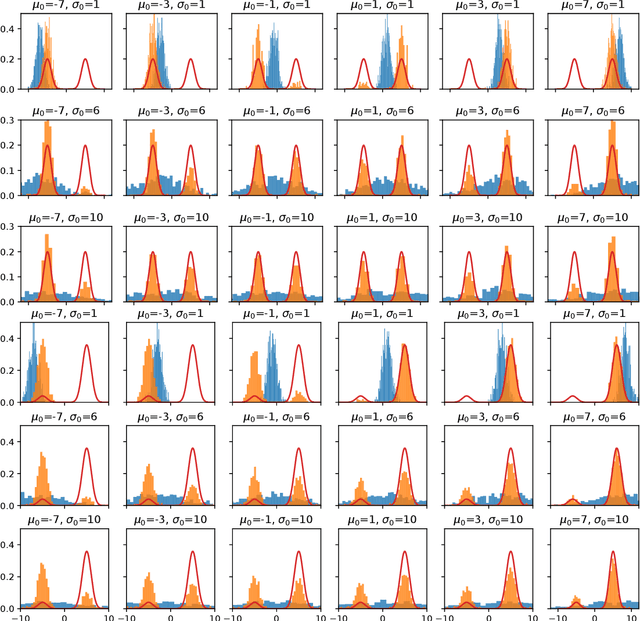
A large family of score-based methods are developed recently to solve unsupervised learning problems including density estimation, statistical testing and variational inference. These methods are attractive because they exploit the derivative of the log density, which is independent of the normaliser, and are thus suitable for tasks involving unnormalised densities. Despite the theoretical guarantees on the performance, here we illustrate a common practical issue suffered by these methods when the unnormalised distribution of interest has isolated components. In particular, we study the behaviour of some popular score-based methods on tasks involving 1-D mixture of Gaussian. These methods fail to identify appropriate mixing proportions when the unnormalised distribution is multimodal. Finally, some directions for finding a remedy are discussed in light of recent successes in specific tasks. We hope to bring the attention of theoreticians and practitioners to this issue when developing new algorithms and applications.