Controlling Moments with Kernel Stein Discrepancies

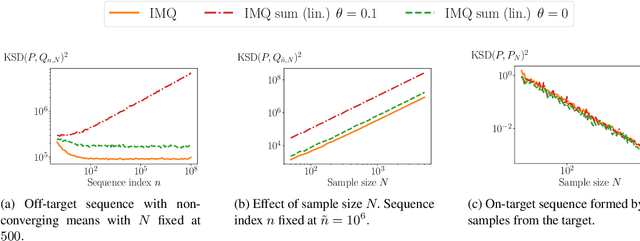
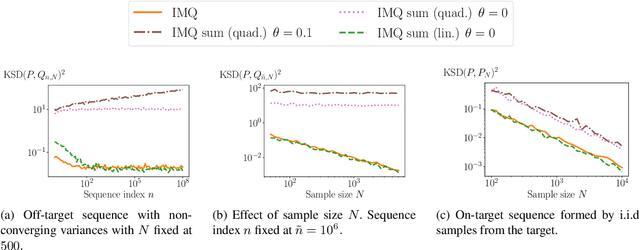
Quantifying the deviation of a probability distribution is challenging when the target distribution is defined by a density with an intractable normalizing constant. The kernel Stein discrepancy (KSD) was proposed to address this problem and has been applied to various tasks including diagnosing approximate MCMC samplers and goodness-of-fit testing for unnormalized statistical models. This article investigates a convergence control property of the diffusion kernel Stein discrepancy (DKSD), an instance of the KSD proposed by Barp et al. (2019). We extend the result of Gorham and Mackey (2017), which showed that the KSD controls the bounded-Lipschitz metric, to functions of polynomial growth. Specifically, we prove that the DKSD controls the integral probability metric defined by a class of pseudo-Lipschitz functions, a polynomial generalization of Lipschitz functions. We also provide practical sufficient conditions on the reproducing kernel for the stated property to hold. In particular, we show that the DKSD detects non-convergence in moments with an appropriate kernel.