A kernel Stein test of goodness of fit for sequential models
Paper and Code
Oct 19, 2022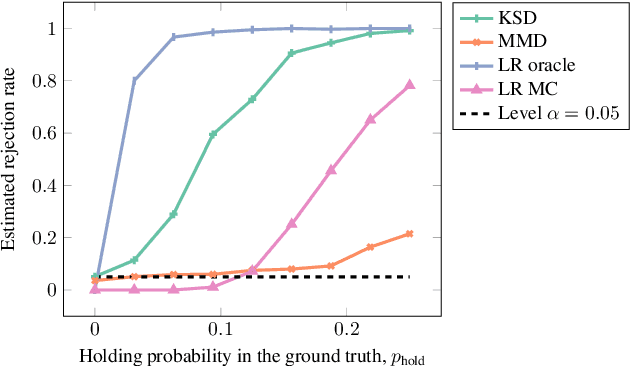
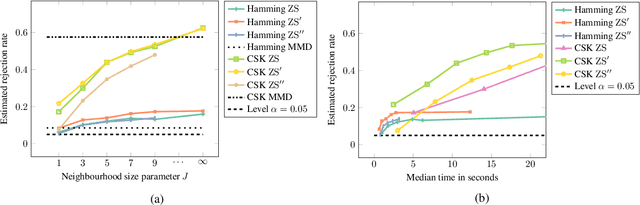
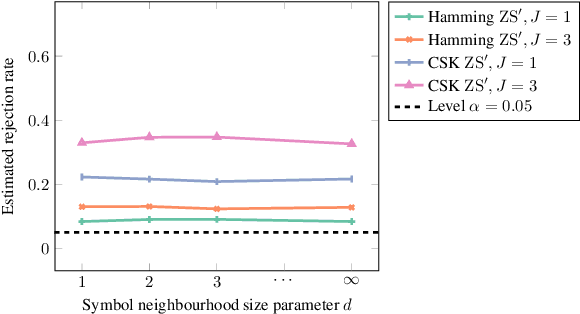
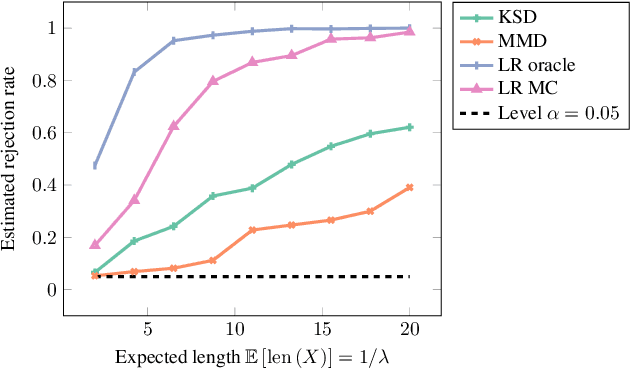
We propose a goodness-of-fit measure for probability densities modelling observations with varying dimensionality, such as text documents of differing lengths or variable-length sequences. The proposed measure is an instance of the kernel Stein discrepancy (KSD), which has been used to construct goodness-of-fit tests for unnormalised densities. Existing KSDs require the model to be defined on a fixed-dimension space. As our major contributions, we extend the KSD to the variable dimension setting by identifying appropriate Stein operators, and propose a novel KSD goodness-of-fit test. As with the previous variants, the proposed KSD does not require the density to be normalised, allowing the evaluation of a large class of models. Our test is shown to perform well in practice on discrete sequential data benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge