Testing Goodness of Fit of Conditional Density Models with Kernels
Paper and Code
Feb 24, 2020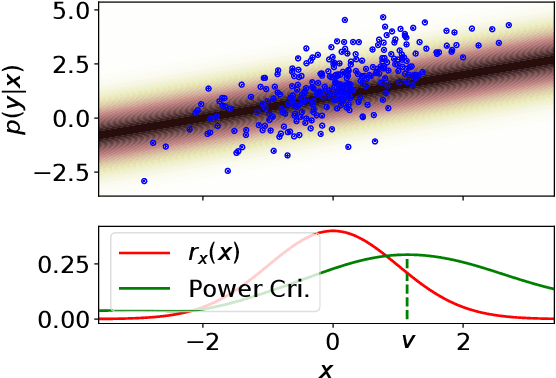
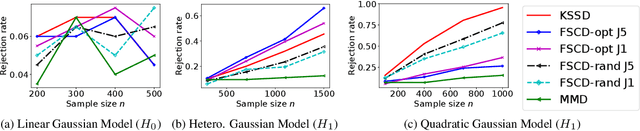
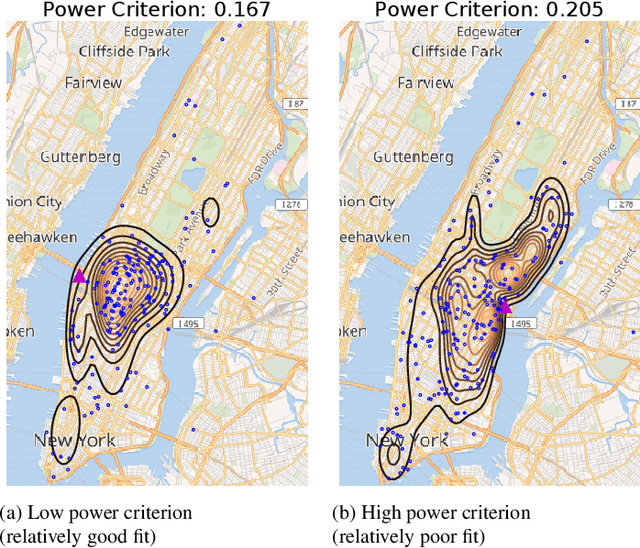
We propose two nonparametric statistical tests of goodness of fit for conditional distributions: given a conditional probability density function $p(y|x)$ and a joint sample, decide whether the sample is drawn from $p(y|x)r_x(x)$ for some density $r_x$. Our tests, formulated with a Stein operator, can be applied to any differentiable conditional density model, and require no knowledge of the normalizing constant. We show that 1) our tests are consistent against any fixed alternative conditional model; 2) the statistics can be estimated easily, requiring no density estimation as an intermediate step; and 3) our second test offers an interpretable test result providing insight on where the conditional model does not fit well in the domain of the covariate. We demonstrate the interpretability of our test on a task of modeling the distribution of New York City's taxi drop-off location given a pick-up point. To our knowledge, our work is the first to propose such conditional goodness-of-fit tests that simultaneously have all these desirable properties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge