Orthonormal Expansions for Translation-Invariant Kernels
Paper and Code
Jun 17, 2022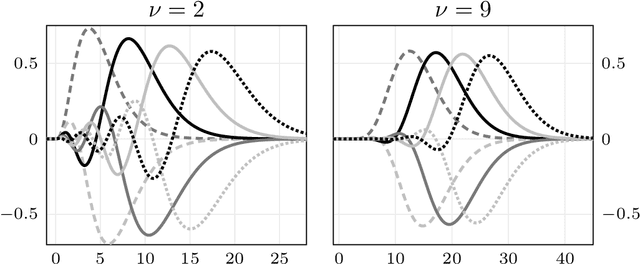
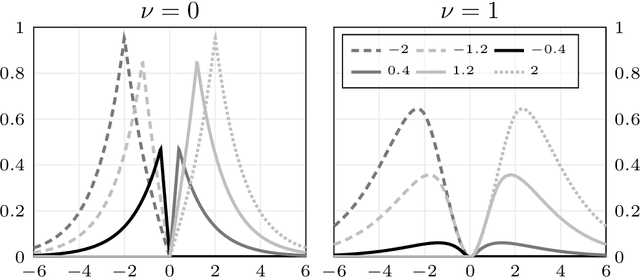
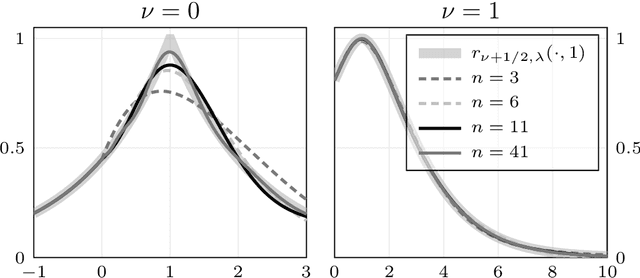
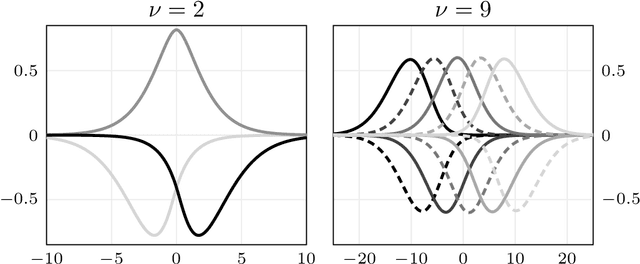
We present a general Fourier analytic technique for constructing orthonormal basis expansions of translation-invariant kernels from orthonormal bases of $\mathscr{L}_2(\mathbb{R})$. This allows us to derive explicit expansions on the real line for (i) Mat\'ern kernels of all half-integer orders in terms of associated Laguerre functions, (ii) the Cauchy kernel in terms of rational functions, and (iii) the Gaussian kernel in terms of Hermite functions.
* 23 pages, 8 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge